QUIZ 3 
SAMPLE EXAM 1 WORKSHEET
SAMPLE EXAM 1 SP'11
SAMPLE EXAM 1 FALL'12
SAMPLE EXAM 2 FALL'12, SEE PROBLEMS 1 AND 5 FOR TEST 1 EXTRA CREDIT EXAMPLES FROM CHAPTER 3 ON RELATIVE AND CIRCULAR MOTION. PROJECTILE MOTION IS REQUIRED. **SCROLL DOWN TO THE BOTTOM OF THE PAGE TO SEE THE SOLUTIONS.**

VIRTUAL LAB SIMULATION

Turn in the following exercises/problems next week: Ch. 2 Free Fall exercise/problems 35, 40, 41, 44, 48, 47, 80, 81, 84 ,88, 87, 89.  (*DISCUSSIONS PROVIDED  SO FAR; some problems may not have discussions but still are due.)

COMMENTS:  As a rule of  thumb, graphs as in #88 and #87 are especially helpful  in problems with two moving objects. This would apply to quiz 2 as well. 
MORE DISCUSSIONS TO FOLLOW: CHECK BACK FREQUENTLY
44.  Study Problem 89, especially part (a),  discussion below in detail. Notice differences and similarities. In particular  compare the sandbag's motion with the helicopter's  after  shut off or  Austin Powers' trajectory after he "steps off" copter such that his  initial velocity in free fall, before turning on  jets, is up relative to  ground.  Same equations/formulae. In both problems,  Austin Powers and sandbag  move upward initially relative to ground despite "stepping off" with zero velocity with respect to  rising vessel.  
80. SOLVE A VERTICAL  FREE FALL  EQUATION FOR TIME OF FLIGHT OF EGG. THEN SUBSTITUTE INTO PROFESSOR'S UNIFORM HORIZONTAL MOTION EQUATION.
12th edition and 13th edition correspondence:  39..35, 40...40, 41...41, 44...44*,  48....48, 49....47, 76.....80*, 77....,81,  80........84*, 84.....88*, 85....87*, 86...89*.
84. SET  UP THE SYSTEM OF EQUATIONS FOR THE PROBLEM.  TIP: LET DOWN BE POSITIVE. Thus a = +g.  Set the top level (windowsill)  to be Y1 = 0 , the top of  the window  at Y2 and the bottom of the window at Y3. Note: Since the pot was dropped, V1 = 0. You are given  1.90 m = (V3 + V2)*(0.420 s) /2  and you also know  
V3 = V2 + g*(0.420 s) .   Solve these two equations simultaneously   for V3 and V2.  Then use Y2 - Y1 = V22/(2g).

Note:  t3 - t2 = 0.420 seconds.

YOU CAN ALSO FIND THE SOLUTION USING ANOTHER SET OF EQUATIONS RELYING MORE ON TIME.
I.E.,  Y3 - Y2 = 1.90 m =  V2*(t3 - t2)+ (1/2)*g*(t3  - t2)2  from which you can get V2, requested quantity.

THE PROBLEM COULD BE RELEVANT IN A CRIME OR INSURANCE INVESTIGATION: For example investigators  are trying to find V2 to determine the speed of t pot at impact with someone injured while walking on ground below.
88**. Let down be the  positive direction of motion.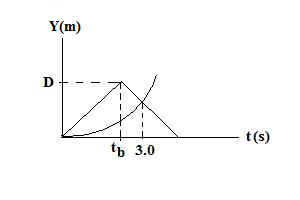

The triangular  shape represents the  sound's motion, tb the time it takes sound to get to bottom, 3.0 seconds  the time it takes sound and professor to meet while she moves downward in positive direction, and D the cliff's height.   The parabola represents her free fall   motion.  The slope of inclined triangular  sections are + 340 m/s and - 340 m/s moving right in time, respectively.  Solve for D = 340*tb. Use  information to find  tb, geometrically if necessary. 3.0 seconds is the time when the two objects have the same  X; use properties of lines,  parabolas vertexed at origin. 

FURTHER COMMENTS:
Think of  a horizontal one dimensional race of sorts between a sound pulse and someone speeding up to the right with acceleration 9.8 m/s^2.  As soon as I start I send a sound signal in the forward direction toward a vertical wall at the far right.. That signal will bounce off the wall and pass through me as it moves in the opposite direction and I move in the initial direction toward the wall. An echo. The shape of the sound signal's position vs time  will be a triangle. Like a pyramid.  As you move to the right in time, the pyramid slopes upward at an incline whose tangent equals the speed of sound. At  peak of pyramid, the sound  hits the wall, and as the pulse returns in the opposite direction, the curve traced out is a straight line with decreasing values of D  as you move  away from peak in time—the slope of this segment is the negative of the speed of sound. Find the intersection of pyramid segment and  parabola representing your position vs time  given by (1/2(*g*t^2.

This requires some care since mathematically it could be on either side of the peak in time. To the left of the peak in time  means we catch up with the sound, highly unlikely and mathematically impossible since the speed of sound is over 300 m/s and we start from rest. In theory I could catch up with the sound if someone launched me with huge initial velocity  from a strong enough spring loaded cannon (LOL).  So the intersection is to the right of the peak in time. Use the equation  of a line with negative slope -340 m/s. The intersection between the parabola and that line segment happens at 3 seconds.

The value of the pyramid will be D – 340*(t – tb), where tb is the time it takes the sound to hit the bottom,  t = 3 seconds and D is the depth of the cliff whose bottom  the sound hits. You have :

D – 340*(t – tb)  = (1/2)*gt2, where t = 3 seconds. .


We need to find D and we will know everything we need to know about the situation. But D = 340*tb . Thus, 

 340*tb – 340*(t – tb) = (1/2)*gt2   from whence you get tb and finally D.

NOTE: THE DIAGRAM ABOVE IS NOT TO SCALE AND SHOULD BE RE-DRAWN TO BETTER REFLECT THE SITUATION.  IN PARTICULAR, THE PICTURE LOOKS MORE LIKE THIS:

NOTE THE POOR PROFESSOR, WHO   REPRESENTS THE PARABOLA ABOVE,  REACHES DEPTH D IN A TIME OVER THREE TIMES 3.0 SECONDS, THE INSTANT HE/SHE  HEARS THE ECHO.

THE TWO DOTS REPRESENTS A CONTINUATION OF THE PARABOLA TO THE POINT WHERE PROFESSOR HITS GROUND, the parabola reaching  value D.  (HOPE A TRAMPOLINE ALLOWED HIM/HER  TO SURVIVE---MAYBE HE/SHE  LANDED ON REALLY SOFT PILLOWS!).  
87. Let up  be the positive direction. (a) and (b) are basic as is (d) once you get (c):

(c)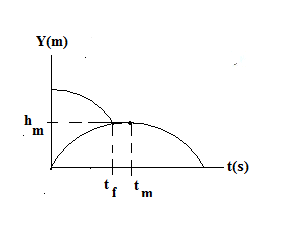


 

At time t = 0, the first ball is dropping from rest downward from height 3.0 m and second ball is thrown upward with speed equal to two-thirds the  value computed in part (a).   Two parabolas are shown , vertexed at point (0, 3.0),  where 3.0 is in meters (m)  and at (tm, hm), where tm and hm are the time and value of  maximum height reached by  second ball. Solve for tf, the time when they pass.
(d) y = (2/3)*v1 - (1/2)*g*t2. , where t  is  time from  part (c) and  is  velocity from part (a) 
89. SYNOPSIS OF HINT TO #89 PART (b). NOTE: t^2 means t2. FOR PART (a), see the methods of #44 above.


# (a)  THE HELICOPTER SHUTS OFF ENGINES AT A HEIGHT Y2 OF 250 m = (1/2)(5)(10)2. AT
THAT MOMENT THE HELICOPTER HAS VELOCITY V2 = (5)*(10) = 50 m/s. THIS
IS ALSO THE INITIAL HEIGHT AND VELOCITY OF AUSTIN POWERS WHEN HE STEPS
OFF THE COPTER; FROM THIS INFO YOU CAN GET THE MAXIMUM HEIGHT REACHED BY COPTER AND POWERS, WHO ARE BOTH IN FREE FALL AND MOVE TOGETHER BEFORE POWERS TURNS ON HIS "JET PACKS." HE  TURNS ON HIS JET PACKS AFTER HE AND COPTER REACH MAXIMUM HEIGHT AND ARE BOTH MOVING DOWN.

# (b) YOU CAN FIND EASILY THE TIME t   IT TAKES THE COPTER TO CRASH AFTER
SHUT OFF: SOLVE
-250 m = = 50 m/s*t - (1/2)*gt2   TO GET t = 13.9 seconds after the
engines are shut off. (Adding 10 seconds, 23.9 s after take off.)
--------------------------------------------------------------------------------------
# NOW FIND THE HEIGHT OF POWERS WHEN THE COPTER CRASHES, ASSUMING HE
TURNS ON HIS JET PACKS 7 SECONDS AFTER SHUT OFF. THAT HEIGHT IS SIMPLY
H =  Y(AT 7 SECONDS)  + V3'*(t - 7)  - (1/2)*(2 m/s^2)*(t - 7)2, where
t - 7 = 13.9 s - 7 s = 6.9 seconds  and V3' HAS A PRIME ' TO DISTINGUISH POWERS FROM COPTER,
V3' = (50 m/s) - g*(7 s) = -18.6 m/s. You complete computation of H by
noting Y(AT 7 SECONDS) =
 250 m  + (50 m/s)*(7 s) - (1/2)g( 7s)2 = 360 m. Thus, H = 360 m - (18.6)(6.9) - (1/2)*(2)*(6.9)2 = 184 m above ground, over 540 ft high  !
---------------------------------------------------------------------------------------
COMMENTS/MORE HINTS:
Let up be the positive direction. Thus, a = -g for the free fall parts.  Be careful with the velocity signs: when motion is up, velocity is positive,  otherwise it's negative. 

Like a chapter from the Hollywood set of Iron Man,  the helicopter rises for 10.0 s at  acceleration a = 5.0 m/s^2.  You can immediately  find copter's vertical distance at 10.0 seconds by evaluating Y2 - Y1 = 
V1*(t2  - t1) + (1/2)*a*(t2 - t2)^2, where a = 5.0 m/s^2, Y1 = 0,  V1 = 0, t2 = 10.0 seconds, and t1 = 0.  For  copter velocity at 10.0 sec: V2 = V1 + a*(t2 - t1). Note: Acceleration a and V2 are both positive.
--------------------------------------------------------------------------------------
This is the main set up. The  rest is  straight-forward once you find V2 and Y2 above.  At 10.0 seconds, copter engine shuts off, free fall begins and  problem is identical  to earlier exercises (like #44)  involving throwing a ball upward with initial velocity V2 from height Y2.  After shut off, you can find the time period  it takes copter to crash by  solving for 
t3 - t2:
Y3 - Y2 = V2*(t3 - t2) - (1/2)*g*(t3 - t2)^2, where Y3 = 0, and V2, Y2 are derived earlier. 
--------------------------------------------------------------------------------------------------------
THE SYMBOL PRIME ' DISTINGUISHES POWERS FROM COPTER. Among other  things, you are asked to find Powers' location above  ground when copter crashes after  time period t3 - t2.  After 10.0 seconds of  COPTER'S flight, we can reset our stop watch to ZERO. Note  when Powers "steps off"  copter, he has upward velocity V2 relative to an observer ON GROUND. Find the Power's displacement after 7.0 seconds of flight in free fall (before turning  jet packs!) :

Y3' - Y2 = V2*( 7.0 s)  - (1/2)*g*(7.0 s)^2, where Y3' is primed to distinguish Powers from  copter.  Note you must add Y2 to this displacement to get Powers' distance above ground.

To get Power's additional  displacement after activating jets,
Y4' - Y3' = V3'*(t4' - t3') - (1/2)*(2.0 m/s^2)*(t4' - t3')^2 ,  where t4' - t3' = time interval  between igniting  jets and copter's impact with ground.  Clearly t4' - t3' = (t3 - t2) - 7.0 s.  Note: V3' = V2 - g*(7.0 s) .  To get distance above ground  add Y3' = 360 (m).