QUIZ 6  (REAL EXAM 2)
ANSWERS
SAMPLE TEST 2
QUIZ 6  IS MORE CLOSELY  EXAMPLE DRIVEN---HERE WILL BE A CLOSE CORRESPONDENCE,  often with explicit cross indexes,  BETWEEN EXAMPLES  5.1 TO 5.24 AND THE EXERCISE/PROBLEMS.  THESE PROBLEMS HELP US UNDERSTAND  APPLICATIONS OF NEWTON'S LAWS, WHICH IN TURN  OPEN  US   VIA ANALOGY TO  DEEP INNER-WORKINGS OF NATURE. FOR EXAMPLE  CLASSICAL MODELS STARTING WITH THESE PROBLEMS HELP US VISUALIZE  MOLECULAR PROCESSES  OBEYING  NON-INTUITIVE STATISTICS. Sometimes it helps to think of an electron  orbiting in a well defined, classical circular orbit around the nucleus  using this  chapter's definition of centripetal force even though we know  electrons come in waves  or "clouds" with a  probability function  and   UNCERTAINTY PRINCIPLE . 
DISCUSSION QUESTIONS 12*, 13*, 16*, 19*, 20*, 23*, 24*, 25*, 26*, 27*, 28*, 29*, 30* 
EXERCISES/PROBLEMS: 
SEC. 5.1 (EQUILIBRIUM, STATIC OR DYNAMIC):  2*, 6( Try also 56,  8, 9)
 34, SEE EXAMPLE 5.4, 60 (Try 59), 34;

SEC  5.2 (DYNAMICS):  #68*, A WARM UP PROBLEM,  WHICH HAS A FAMILIAR
GEOMETRY (CLASS NOTES) AND ILLUSTRATES  NON-EQUILIBRIUM CONDITIONS;
ALSO DO 12*, 14*,  16* , 17* (Try 15*) , 34* , 35*,  19*, 20*  ;

SEC. 5.3 (FRICTION AND  AND/OR MORE COMPLICATED SITUATIONS): 26* , 29*
(Try # 26*),  69*  , 36* , 38* , 41* , 40* ;

EXTENSIONS OF YOUR KNOWLEDGE BASE: (Try 97* and 122*, 123*)
NOTE: #97* IS EXTREMELY IMPORTANT  IMPORTANT  FOR REASONS THAT CRYSTALLIZE AFTER TODAY.
2*. You can also assume in each block  is moving at constant speed along the lines of their motion, which means the acceleration equals zero. This is called DYNAMIC EQUILIBRIUM. In either case AT REST OR WITH CONSTANT SPEED,  with mass m,   EACH BLOCK has acceleration equal to zero , so you can  simply write

sum of forces in y dir = pos - nag = 0 since the  acceleration in y direction = 0,

In  (a) for example ,we have 0 = pos - neg = T - mg.

6*.  Form an x-y axes on the plane of you page and let right and upward  on paper be the pos x and pos y directions, respectively. ISOLATE MASS A.
sum of force in x dir = 0 = -TA*cos0 + TB*cos theta, where theta is the angle the B string makes with the pos x-axis.
sum of forces in y dir = 0 = TB*sin theta  - mg
8*. See #4,  Ch. 4 to compare. DRAW YOUR AXES DIFFERENTLY NOW WITH an x-y axes on the plane of your page and let UP the incline  be the pos x direction and let PERPENDICULAR  and away from the incline surface  be the  pos y direction.
sum of forces in x direction = 0 =  T*cos31 - mg*sin 25.
sum of forces in y direction = 0 = T*sin 31 + N - mg*cos 25.
From this info you can answer all questions selectively.
DRAW A FREE BODY DIAGRAM.
9*. . DYNAMIC EQUILIBRIUM MEANS MOTION WITH ZERO ACCELERATION AS IN THIS CASE. DRAW YOUR AXES  NOW WITH an x-y axes on the plane of your page and let DOWN the INCLINE be the pos x direction and let PERPENDICULAR  and away from the INCLINE surface  be the  pos y direction.
(a)   
sum of forces in x direction = 0 =   mg*sin 11 - F
sum of forces in y direction = 0 =  N - mg*cos 11
(b)
sum of forces in x direction = 0 =   mg*sin 11 - F*cos 11
sum of forces in y direction = 0 =  N - mg*cos 11 - F*sin 11; Note in the increase in N from  part (a) case.
DRAW A FREE BODY DIAGRAM.
SPECIAL PROBLEM 1(Test 2 review):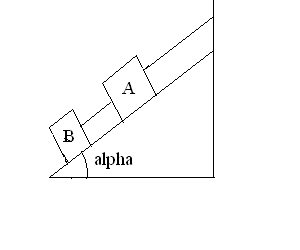
 FIND THE TENSION IN THE ROPE CONNECTING  (a) BLOCKS A AND B (b)   BLOCK A  TO WALL.  See Example 5.4 . To get the tension in the rope connecting A to the wall, you can assume that the that rope supports a total mass MA + MB. Thus TA = (MA + MB)*g*sin alpha, , where alpha is the angle with the horizontal. To find TB, isolate   MB. : Let the x axis be along the incline so that  sum of forces in x direction = 0 =  TB - MB*g*sin alpha. For the normal forces in both cases we have:
sum of forces in y dir = N = M*g*cos alpha 
60*.. DRAW YOUR AXES DIFFERENTLY NOW WITH an x-y axes on the plane of your page and let UP the plane be the pos x direction and let PERPENDICULAR  and away from the plane surface  be the  pos y direction. APPLY THE FORCES AT THE BALL CENTER.
The tension exerts a force parallel to the horizontal , so it is like #9, part (b).
DRAW A FREE BODY DIAGRAM.
sum of the forces in x direction = 0 = pos - neg =  T*cos35 - mg*sin 35
sum of forces in y direction = 0 =  N - mg*cos 35 - T*sin 35
12*. See example 5.9. Let the power supply play the same role as the woman. Note  the difference. In this problem the rocket moves up and accelerates upward ( speeds up ) whereas in the example, the elevator slows down while moving down, which means the acceleration also points up. So the acceleration is the same but the motions are  different between the example and this problem.   If up is positive for the motion, you'd write after isolating the power supply:
For part (b), m*a = pos - neg = N - mg, where m is the supply's mass and N is the magnitude of the normal force on it. Note:
For part (a), (m + M)*a = F - (m + M)*g  where F = 1720 (N) and M + m is the sum of the rocket's and POWER SUPPLY'S  mass.
14*..   See notes to capture the idea of  two  mass-less strings connecting 3 blocks together as they moved with common acceleration under the influence of an external force of magnitude F. Formally,  in this problem you'll have three equations and three unknowns, acceleration a, and TA and TB. ISOLATE EACH MASS !
16*.
(a) See class notes: Sum of the forces in the x dir = m*a = pos - neg = m*g*sin theta.  DRAW YOUR AXES  NOW WITH an x-y axes on the plane of your page and let DOWN the incline  be the pos x direction and let PERPENDICULAR  and away from the incline surface  be the  pos y direction. You can  get acceleration a from Ch. 2 theory.
(b)  Add friction and the equation becomes: Sum of the forces in the x dir = m*a = pos - neg = m*g*sin theta. - f, where f = 10.0 (N).
17*.  See example 5.12.
19*. Nice problem,  harkening back to example 5.2 for a string with mass.    Let upward be the +y direction.  Let a lifting clamp labeled A  meet the   top of the chain at point A.  Label the chain S just like I've done and the boulder B. Use the same notation as notes but remember each object-- boulder B and the chain S--have a downward gravitational force on them. For example the string  equation reads
ms*a = FSA - FSB  - ms*g. The boulder equation reads:
mB*a = FBS  - mB*g. Note FSA = the tension at the top of chain S = force of the clamp A on  chain. Note: FBS = the tension in  string at the bottom. Note :  FBS=  FSB from Newton's 3rd Law.

Now, if loading is done in dynamic equilibrium at constant speed directed upward, a = 0. Thus: FSA =  FSB  + ms*g  and   FBS  = mB*g. You can now find FSA and FBS .   Note: Theoretically the tension at the midpoint of chain is   (FSA + FSB )/2.

For the problem at hand, let's consider the case when loading is not in equilibrium and  upward acceleration a is greater than zero.
Return to equations:

ms*a = FSA - FSB  - ms*g. 
mB*a = FBS  - mB*g.
Set FSA  =   2.50*ms*g.  Solve for a.
(b) Ch. 2.
20*. The main thing is finding out  if the magnitude of the scale force reading is larger or smaller than the student's normal weight mg. The scale force reading is equal to  magnitude N of the normal force on the student.   If N >mg, the elevator is accelerating upward. If N < mg, the elevator is accelerating downward.

Assume the motion  and thus the positive direction are upward  without loss of generality.
In that case: sum of forces =  m*a =  pos - neg = N - mg. Thus,
N = m*a + mg.  
If acceleration a is positive, the acceleration is upward, thus a > 0 and N >mg. If a is negative, acceleration is downward, thus a < 0 and N < mg . 

(a) N = 450 (N).  Find a. 
(b) N = 670 (N).  Find a
(c) If N = 0  what is a? Should the student be worried? Explain.
(d) To find the tension T in the cable, write sum of forces =  pos - neg for the entire system of elevator and student:
(m + M)*a = T - (m + M)*g, where M is the elevator's mass. Solve for T in parts (a) and (c).
26*. See section 5.3 and  figure 5.19's  narrative.
29.* SEE  figure 5.19 narrative.
(a) fsMAX = 313 (N) = us*N;  fk = 208 (N) = uk*N.
(b) m*a = pos - neg = F - fk ,  where a = 1.10 m/s^2.
(c) Repeat if  g = 1.62 m/s^2.
69.*. Read page 151 about rolling friction.  Use CH. 2 methods friction with constant acceleration, THIS TIME NEGATIVE,  found from Newton's 2ND Law: 
m*a = - pos - neg, where pos = 0 in the case when the  net  horizontal force, pointing in the negative direction, is due to rolling friction  only.
36.*  Examples 5.16 and 5.17. NOTE FOR PART (a), use the coefficient of static friction.
38.*. Example  5.15.
41.*. Example 5.18 (sec. 5.3); NOTE: TERMINAL SPEED IS PROPORTIONAL TO THE SQUARE ROOT OF YOUR WEIGHT, SO THE HEAVIER YOU ARE, THE LARGER YOUR FINAL SPEED (FOR THE SAME D) WHEN  NET FORCE VANISHES; SEE EQUATION 5.13.
40.* Let the positive y direction be up. Let a be the y component of acceleration. In both cases set v = vterm/2, where vterm is the terminal speed of section 5.3  The magnitude of the air resistance force is R= b*v2, proportional to the speed squared.
(a)  sum of forces in y dir = m*a = pos - neg = 0 - mg - R, where R= b*v2.
(b)  sum of forces in y dir = m*a = pos - neg = R - mg,  , where R= b*v2.                          .