|
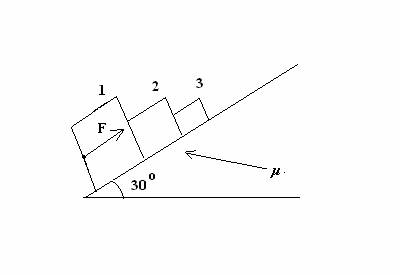
1. ( 40 points) Block 1 , Block 2 and Block 3
are in contact on a table inclined by θ= 30 degrees with the horizontal.
Starting from rest, you apply a force to Block 1 of magnitude F =
101.25 N and direction parallel to incline. As shown below, we represent the
force’s application point with a tail
at Block 1’s left end. The coefficient of kinetic friction between surface
and blocks is µ =
0.15. The block’s masses are m1 = 4.00 kg, m2
= 2.00 kg and
m3 = 1.00 kg, respectively.
To most clearly show your
thinking, try to use these and possibly other well established symbols until the last step before your numerical
answer, which you should box.
For parts (a), (b) and (c) label all vector components with symbols.
(a) (3 points)
Draw a force diagram for Block 1.
(b) (3 points)
Draw a force diagram for Block 2.
(c) (3 points)
Draw a force diagram for Block 3.
(d) (11 points)
What is the magnitude F12 of
the force of
contact between Block 1 and Block 2.
(e) (11 points)
What is the magnitude F23 of
the force of contact between Block 2 and Block 3.
(f) (5 points)
What is the common acceleration of the three blocks?
(g) (3 points)
What is the common velocity of the
three blocks after 3.00 seconds?
----------------------------------------------------
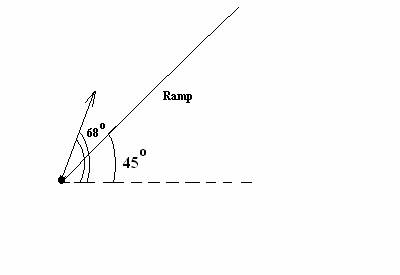
2. (40 points) This
problem deals with a game at an urban golf park.
At t = 0, a golf
ball is launched from
the base of a ramp making a 45 degree angle with the horizontal. The golf ball is launched at speed 20.00 m/s at an angle of 68.0
degrees with the horizontal.
(a) (30 points) How far away does the ball land, measured along the ramp, from the base ? In other words, what is the
distance from the base along the ramp?
(b) (10 points) What is the ball’s speed just before impact with ramp?
-----------------------------------------------------------
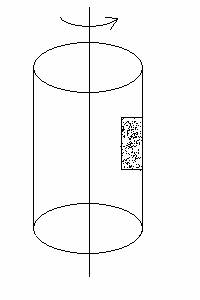
3. (40 points) Below is an engineer’s diagram of a “Rotor-ride” at a carnival. People
rotate in a vertical cylindrically walled room. A typical person is represented
by the grey box. When the floor drops out from under her feet, the person is pinned
against the wall and does not slide
down as she rotates. Let the coefficient of static friction
between person and
wall be µ = 0.400.
(a) (4 points) Draw a free body diagram for the person at the moment
shown.
(b) (30 points) Find the minimum linear speed V of the person
that keeps her from slipping down.
(c) (6 points) Suppose a typical teenager has mass m =
70.00 kg. What would be the magnitude N of the normal force acting on her if she rotated at the speed
you computed in part (b)? Does this seem reasonable? Explain.
|


