QUIZ 5  (REAL EXAM 2 )
ANSWERS
SAMPLE TEST 2
CH. 4--EXERCISES./PROBLEMS  4, 10, 11, 14, 23, 28, 29, 31, 32, 37, 38, 43, 44, 46, 54 ; GO HERE FOR A LIST OF STANDARD PROBLEMS. 
  READ ALL BOOK EXAMPLES SINCE SOME ARE LIKE DISCUSSIONS TO QUIZ PROBLEMS BELOW ! FOR EXAMPLES OF  FORCE DIAGRAMS SEE SECTION 4.6 AND OTHER SECTIONS AS NEEDED.

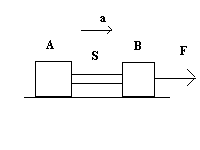
ICQ (TO BE DISCUSSED IN CLASS)  FIND acceleration x-component  a, FSA and FSB in terms of the applied force magnitude F and the masses of box A, box B and  string S. NOTE FSA and FSB are the magnitudes of the force on  string S due to box A and box B,  respectively . 


AS A NICE NUANCE READ EXAMPLE  5.2.
4.  See quiz 1.
10.   Done in class; we stated the graph of Vx vs t  would look like the first 6.0 seconds of figure E4.14 qualitatively.
11.  See #10:  Note the graph of this problem looks  like the first  10 seconds of figure E4.14 qualitatively, except  in this particular exercise the force would resume at 5.0 seconds instead of 6.0 s. For the first 2.0 seconds, get the acceleration from Newton's  Second Law.
14.  See class notes and previous discussions. 
28. ADVANCED PROBLEM !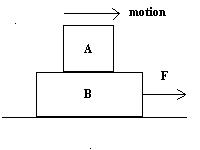
 


Let's examine the two cases below. But before you begin make sure you also isolate Block B and write down the equation of motion for BOTH blocks. In the following,  the symbol "a" represents the x-component of acceleration. We assume the surfaces of contact between the blocks do not move relative to each other (i.e NO  slipping between Box A and B)  Thus,  the only possible force acting on Block A horizontally is the force of static friction  causing A to accelerate to the right. (In A's reference frame, a distant black hole is pulling A to the left, and a rightward static friction force prevents  block from moving left. )  That static friction is a contact force between Block A and B. On A, it acts on  the bottom and is rightward. On B, it acts on the top and is leftward.
(a) 

BLOCK A  :
The net force in the  x direction is :
FXNET = pos - neg. 
 mA*a     = fs  - 0. Again,  fs is the magnitude of the rightward static friction force pulling Block A to the right. 

The net force in the y direction is :
FYNET = pos - neg.  Since the motion is purely horizontal, 
0 = pos - neg = NA - mA*g,  Thus NA = mA*g.  Note: NA is the upward normal force magnitude due to Block B below.

BLOCK B  :
The net force in the  x direction is :
FXNET = pos - neg. 
 mB*a     = F   -  fs .   F is the applied pulling force magnitude and fs is the magnitude of the static friction force (from contact with A) on Block B (due to Block A on top.)  The static friction force on B  is a reaction force to the static friction force on A due to B. 

The net force in the y direction is :
FYNET = pos - neg.  Since the motion is purely horizontal, 
0 = pos - neg = NB - mB*g - NA,   where NB is the normal force of the ground on Block B and  NA  is the downward normal force magnitude on B due to block A, a reaction force to the normal force of B on A. Thus NB = mB*g + NA = mB*g + mA*g  as you might expect.  

Thus the two horizontal equations are :
mA*a     = fs    and
mB*a     = F   -  fs .
 
Note when you add the two equations the static friction force cancels out and you get (mA* + mB)*a     = F  .
Please isolate each block and draw each force on the block in both the vertical and horizontal directions. 

(b)  When there is friction between Block B on the bottom and the ground: 

BLOCK A  :
The net force in the  x direction is :
FXNET = pos - neg. 
 mA*a     = fs  - 0. Again,  fs is the magnitude of the rightward static friction force pulling Block A to the right.  The equation appears to be the same as in (a)  

The y component equation is the same as in (a)

BLOCK B  :
The net force in the  x direction is :
FXNET = pos - neg. 
 mB*a     = F   -  fs   - fk,   where F is the applied pulling force magnitude,  fs is the magnitude of the static friction force (from contact with A)  and fk  is the kinetic friction force discussed later in Ch. 5. 

The y component equation is the same as in (a).

Thus the two horizontal equations are :
mA*a     = fs    and
mB*a     = F   -  fs . - fk . 
 
Note when you add the two equations the static friction force cancels out and you get (mA* + mB)*a     = F  -  fk. 
Please isolate each block and draw each force on the block in both the vertical and horizontal directions. Include the new friction kinetic force fk.

# Finally,  NOW consider the case when F = fk as described in the book in part (b).   In that case we see the acceleration a = 0. 
Please isolate each block and draw each force on the block in both the vertical and horizontal directions. Include the new friction force fk. What would the static friction magnitude fs be in the case when a = 0? Draw diagrams. 
29. This is a classic problem modeling an accelerometer with a pendulum, which are used to regulate pendulum clocks, and are used in scientific instruments such as accelerometers and seismometers. Visit  http://en.wikipedia.org/wiki/Pendulum and see the ball attached to the string.  When the ball hangs vertically straight down, the acceleration is zero; when the string makes an angle with the vertical in a direction opposite the forward motion, the acceleration is not zero.  
31. See the summary page 126 --see (4.7) and (4.8)  diagrams and examples 4.4 and 4.5 in the the body of chapter. This time note the applied force is not horizontal.  Isolate the chair, represented as a block. Assume she moves rightward, the positive direction.

BLOCK :
The net force in the  x direction is :
FXNET = pos - neg.
 mA*a     = F*cos 37  - fk  , where   fk is the magnitude of the leftward kinetic friction force acting on the block.

The net force in the y direction is :
FYNET = pos - neg.  Since the motion is purely horizontal,
0 = pos - neg = N -  F*sin37  - mg.
(a) Please isolate  block and draw each force component on the block in both the vertical and horizontal directions.  Remember to resolve the forces into components along each axis. NOTE:  fk = uk*N, where uk is the kinetic friction coefficient . 
(b)  Solve for the normal force magnitude N. PLUG in  N into the formula  for the friction force magnitude and solve for the acceleration a symbolically.  
32.  See lectures notes.  Let up the incline be the +x direction. Thus along x:
m*a = T - mgisin26.  See example 5.4 but note this problem is somewhat different.   But since the speed is constant, a = 0 just like example 5.4.  
37.
 (a) The net force in the y - direction must be zero in order to sustain the purely horizontal motion (x directed) . Thus:
Fy + F1 *sin 60 - F2*sin30, on pure geometric grounds, where Fy is the y-component of the child's force. One would think the  minimum force  for the  child requires the child's x-component of force Fx = 0.  Solve for Fy. 
(b) FXNET = pos - neg.
m*a =  F1*cos60 + F2*cos30.  Find m and thus mg = weight magnitude..
38.  For the force diagram see example 4.5  Find the magnitude of the acceleration from the 2ND LAW. Then use Ch. 2 methods to find the distance traveled before  stopping assuming the dock is absent.  If that distance is greater than 500 m, find the speed  of the boat at 500 m and determine if there will be boat damage. 
43. WILL BE DONE IN CLASS;.
44. 
(a) WHAT DOES THE  NEWTON'S 3RD LAW  (SCROLL DOWN) LABORATORY PREDICT?
(b) See class notes.
(c)  Use the 2ND LAW on astronaut, where FXNET = m*a = pos - neg. Let the pos direction be toward the spacecraft. Note the only force acting on the astronaut is the reaction force derived from part (a).  Thus neg = 0 in the previous equation.
(d) Same magnitude of  force as on astronaut. Explain; see class notes.
(e) Much smaller acceleration because the spacecraft has a huge relative mass--use 2ND LAW.
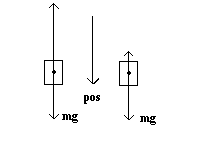
46. Let down be the positive y direction----the direction of motion. Use the equation:
FYNET = pos - neg.
m*a - pos - neg, where a is the y-component of acceleration.
Note:  The magnitude of the positively directed force is mg---that is,  pos = mg.
In the case where the upward thrust force is larger in magnitude than that of the weight, acceleration a is negative and equals  - 1.20 m/s2. See the left picture in the diagram. In the case where the upward thrust force is smaller  in magnitude than that of the weight, acceleration a is positive and equals +0.80 m/s2.  See the right picture in the diagram.

 

 
You will get two equations: m*(-1.20) = pos - neg and m*(0.80) = pos - neg, where you fill in the values for pos and neg in each case. Remember "pos" and "neg"  represent MAGNITUDES.    Let me give some numbers:
 m*(-1.20) = m*g' - 25.0x103 N  and  m*(0.80) = m*g' - 10.0x103 N. Note g' is the unknown value of the gravitational acceleration on Planet X. You have two equations and two unknowns,  g' and m. Find them and compute weight m*g'.

54.  Let upward be the +y direction.  Label the top block B, the bottom block A and the string S. SEE suggested  ICQ (to be discussed later) at the top of this page. Use the same notation as ICQ but remember each object--block B, block A and the string S--have a downward gravitational force on them. For example the string  equation reads
ms*a = FSB - FSA  - ms*g, You will have two other equations, one for block B and one for block A. Solve the three equations for a,  FSB   and FSA  Note: FSB   =   FBS   and   FSA = FAS ,  expressing equality of magnitudes in the action-reaction force of Law 3.