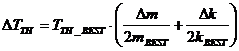|
In this experiment, you measure the parameters --mass m and spring constant k --- of an oscillating system
and check whether the period T is as theory predicts. Consider the mechanical oscillator illustrated in
figures 11-1 and 11-2 of the textbook
(Giancoli) . At equilibrium, the
mass has zero force on it; there the spring is neither stretched or
compressed. When x is negative, the spring is compressed. Otherwise it is
stretched. Fx = -kx is the
x-component force causing the mass to return to the origin (x = 0) at all
times; when the mass moves away from the
origin, it slows down and when it moves toward the origin it speeds up.
This explains all kinds of oscillators, whether they be molecules vibrating back and force in the
warm pen you are using to write your
lecture notes, air molecules oscillating back and force as my
voice travels across the lecture room, or an “up and down” moving piece of
string supporting a transverse standing wave such as on a
guitar string. Such oscillations are everywhere, including your quartz
watch.
In Chapter 11, Newton’s second Law is applied to a mass m
attached to a spring. According to
Newton, the resultant force vector on an object of mass m at a given
moment is m times the acceleration. In Chapter 11, we explored this law in the many
examples in which the force points
towards x = 0. In this experiment you will test the theory for the special case
of a vertically oscillating mass-spring system. The x component of force Fx
= -kx leads to the result that
x= Acos(2πt/T) ,
where A is the amplitude and T is the period.
See section 11-3, especially figure 11-6 and equation 11-8c. On page 292, we discovered :
T TH= 2π·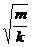 (1) (1)
Note that you may choose the positive x direction to be downward which means x
is positive when the vertical spring is stretched. To test the theory, you will measure the
parameters (Mass m, Spring Constant k
) that appear in the theoretical expression for T to obtain a theoretical value TTh. ---see equation 1. By a timing procedure, you will directly
measure an experimental value TEX, and then compare TTh
with TEX . (See
attached data sheet. ) In particular,
you do the following for the mass-spring system:
(a) Measure the parameters m and k that appear in your expression for the
period in equation (1) and use them to compute TTH.
(b) Measure the time t for a known number of cycles n (n = 10) and compute the
experimental value of the period TEX = t/n. You will measure Tex 5 times and compute the average TEX_BEST.
From this, you will also compute R/N (N=
5) like you did in the lab on
centripetal acceleration; this gives the statistical uncertainty in multiple
measurements when the random errors are
larger than the instrument error in a single, “simple” measurement.
The instrument error is ΔT inst
= 0.001 s /n or 0.0001
s/n ( where n = 10), depending on the timer resolution. The uncertainty ΔTEX you choose will either be ΔT inst or R/N , which ever
is larger. See attached data sheet. In either case, the uncertainty is rounded
to just one digit and we round the average (“best”) value to the same decimal
place.
(c) Compute the uncertainties in the
values TEX and TTH, then test the proposition that TTH
= TEX using the criteria we used in centripetal acceleration lab:
|TEX – TTH| < 2(ΔTEX + ΔTTH),
PROCEDURE
As in figure 11-3, you will hang a tapered spring vertically
from a support with the small end of
the spring at the top. This spring
taper direction is important for an
accurate reading. The narrowing of the spring’s diameter toward the top allows
the spring to stretch uniformly along its entire length. The narrowing toward the top means
the upper half of the spring is stiffer than the lower half. This stiffness “gradient”
is necessary because the
upper part supports the weight of
the lower part and so must be stiffer if
it is to have the same stretch
per unit length as the lower.
(Q-1) You will add a mass of value m = 0.30 kg as suggested in figure 11-3 and
allow the system to oscillate up and
down. Remember, the hanger already has
mass 50 g, so you will add 0.250 kg. The formula for the period is given by
equation (1) but there is one complication that has to do with the correct
value of the mass. While the system vibrates up and down, different parts of
the spring move at different speeds. The effective mass ms,Eff of the spring adds to the system’s
inertia and kinetic energy storage capacity.
It turns out that the mass m
includes both 0.30 kg and one- third of the mass of the spring;
a calculus derivation shows that ms,Eff = ms/3, where ms is the
spring mass. You may enter this
expression under (Q-1) of the attached data sheet.
(Q-2)
Beginning with equation (1), it is easy to derive (using
Math 1 and 3 methods)
the expression for the uncertainty in the theoretical value TTH of the period :
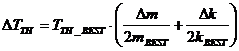
The expression contains the “best “ values from discussions below. Δm and Δk are the uncertainties in the
oscillating mass m and spring constant k discussed below.
(Q-3) To find the value of the spring
constant k, use a sliding caliper jaw to record the position x’ of the bottom
of the weight hanger with weights of mass M = 100, 200, 300 , 400 and 500 grams
(g) suspended from the spring. Plot
values of force in newtons vs x’ in meters and find the spring constant k
in N/m with uncertainty Δk.
Note: The uncertainties in x’ and the
hanging masses M should be very small . Thus, the precision of your value of k will be limited
by the graphing process. Thus, you can proceed without using error bars which
will be discussed in a future lab. The least squares fit computational method
for determining the slope will also be addressed later. The following suggestions are for graphically
measuring, or estimating, the slope k:
(1) Do not try to make the line pass
through any particular data point. Sometimes a line passes through none of
these points. On the other hand, when
the points have very little “scatter”
, the line may seem to go through all
the points. Since you give
greater weight to points with short or no error bars, you will make an
extra effort to pass the line close to
these points.
(2) Extend the line beyond the data points to the right and /or left.
(3) Determine a right triangle,
called the slope triangle. Do this by choosing two points on the graph,
indicating them with arrows, that approximately span the domain of the x’ data.
Compute ΔFs and Δx’.
Compute the slope kbest from their ratio—k = ΔFs / Δx’ . Follow these guidelines
·
(a) Begin and end the Δx’ interval on major
grid vertical lines; major grid lines are
the darker lines that divide the smallest grid divisions into groups of
5 or 10. Do not choose a vertical line
that passes through or very close to a data point. The Δx’ interval should
be rather wide, about as wide as the domain of your plotted x’ values. Draw arrows at the two
intersection points—to be used in computing the slope---where the graph passes
through the two vertical lines.
·
(b) Do not use values from the data table to
compute the slope even if they are from data points that appear to be on or
near the line. Use the two values located at the arrows you drew in (a). They
are determined by the line representing the best information from ALL your
data.
·
(c )In
your slope(k) computation, show the beginning and ending values of x’
and Fs that you read from the graph at the two arrows, by
substituting them into your expression used to find the slope. Note: slope = kbest = rise/run= ΔFs / Δx’.
Since the uncertainties in ΔFs
and Δx’ are so small, the precision is limited by the drawing
process. In this case, you can compute the uncertainty in the slope k like
this:
Δk = lcy/ Δx’, where lcy is the least count of the grid for the y (Fs)
axis and Δx’ is the base of the slope of the triangle used to find kbest .
(Q-4) Weigh the spring to find ms and compute the effective mass ms,Eff. Enter the value mo = 0.30 kg.
Compute the total mass m = ms,Eff + mo. Use this value along with kbest to find T TH = 2π·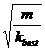
Compute the uncertainty ΔTTH assuming an uncertainty of 1 g for your mass measurements. See (Q-2) and (Q-3).
(Q-5) Suspend 0.30 kg from the spring,
displace it slightly and determine the experimental period TEX.
Make at least 5 trials and count at least 10 cycles for each trial:
You will measure TEX 5
times and compute the average TEX-BEST. From this, you will also compute R/N, where N =
5; this gives the statistical
uncertainty of multiple measurements
when the random errors are larger than the instrument error in a single,
“simple” measurement. The instrument error is ΔT inst = 0.001 s /n or 0.0001 s/n ( where n = 10), depending on the timer resolution. The uncertainty ΔTEX you choose will either be ΔT inst or R/N , which ever
is larger. In either case, the
uncertainty is rounded to just one digit and we round the average (“best”)
value to the same decimal place.
(Q-6) Compare the discrepancy between
the theoretical and experimental values to the sum of their uncertainties.
|