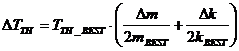(Q-1)

Using calculus, Ms Eff = ms/3, where  is the spring mass.

(Q-2)

Using calculus, it is easy to derive ,

(Q-3)

M(kg)	Fs(N), using g = 9.8 m/s2.	x' (m)
0.100	0.98	51.95  (cm) = 0.5195 (m)
0.200	1.96	61.70  (cm) = 0.6170 (m)
0.300	2.94	71.65 (cm) = 0.7165 (m)
0.400	3.92	81.40 (cm) = 0.8140 (m)
0.500	4.90	91.35 (cm) = 0.9135 (m)

 

Computation of k from the graph: The uncertainties in x’   and the hanging masses M should be very small . Thus, the  precision of your value of k will be limited by the graphing process. Thus, you can proceed without using error bars .  Since the uncertainties in ΔF_s  and Δx’ are so small, the precision is limited by the drawing process. In this case, you can compute the uncertainty in the slope k like this: Δk = lc_y/ Δx’, where lc_y is the least count of the grid for the y (F_s) axis and Δx’ is the base of the slope of the triangle used to find   k_best  .

From what we have discussed in  class, your drawing in the y-direction should have every 20 small divisions be equal  to 1.0 (N) .  Thus, each small division in the y direction equals  0.05 (N). This number, in combination with the  base of the triangle Δx’, will give you Δk= lc_y/ Δx’.   See the previous paragraph. 
The horizontal scale has 20 small division equaling 0.1000  m. Thus, one small horizontal unit equals 0.005 (N).

Follow the steps in the hand out while graphing;  I am skipping the beginning steps on errors bars given the expected good precision. See page 59, Step 4. Try to make a small circle around each point, two or three mm in diameter, centered at the dot.  Since there are no expected error bars you could skip to 60, Graphical Slopes . (See fig. 5.4--Getting the best slope.) Step 6 emphasizes not trying to make the line pass through any particular point, though if the points line up well, it may be difficult avoiding going through many or all the points.  Remember to extend the line beyond the data points to the left and right. (Step 6. c. ). In Step 7, you read about determining a right triangle, called the slope triangle. Here is how you draw: Choose two points on the graph,  indicating them with arrows approximately spanning the domain of the data. The slope equals the rise/run. 

a. Here are guidelines for the  run . The run should begin and  end on major vertical grid lines. for example 0.5000 m and 1.0000 m marks. The run should be rather wide, about as wide as the domain,  as in the  above mentioned choice of vertical major gridlines  for the run.

d. Show the beginning and ending values of x and y,  in this case x' and  F_s , that you read at the two arrows. Substitute these values into your expression for the  slope = rise/ run.  Note that a point has an inherent ( "simple") uncertainty (1/4)*(0.005) = 0.00125 = 0.001 to one sig. fig in the x direction and  (1/4)*(0.05) = 0.0125= 0.01 to one sig . fig.  in the y direction. What this basically means is that you are rounding  to the nearest small division. Include units.  Do not round off  since you will be using the slope k  in intermediate computations.   Here is what I report for the above  sample data.  
 k_BEST =  (4.80  - 0.80)/(0.900 - 0.500) = 4.00 (N)/ 0.400 (m) = 10.0 N/m.  

We might as well compute the uncertainty in k = Δk= lc_y/ Δx’ = 0.0125/0.400 = 0.03125.  We will use that under (Q-5) for the uncertainty in theoretical T. 

(Q-4)

masses related to total mass m
ms	171.90  = 0.17190 (kg)
msEFF	57.350  = 0.57350 (kg)
mo	300.00  = 0.30000 (kg)
mBEST	357.350  = 0.357350 (kg)

Note that the uncertainty in each measurement is considered to be 1 g.   Thus Δm_s = 1 g and Δm_o = 1 g. Since m =  m_sEFF  + m_o,  Δm  =  1g + 1 g/3 = 1.33333 g = 1 g if rounded to one sig. fig.

CORRECTIVE  NOTE: This last conclusion may be an overestimation and lead to conceptual inconsistencies since you used a mass scale which has a smaller uncertainty than 1 g.  In the centripetal force lab, we said the uncertainty in mass scale measurements is  (1/4)*(0.1 g) = 0.025 g = 0.03 if rounded. So a better approximation would be Δm = 0.025 + 0.025/3 = 0.03333 = 0.03 g if rounded down.  This dovetails with the 1/100th place precision of the mass.
 
(Q-5)
We are now in the position to  find the theoretical period given by formula (1): 
T = 

 2π· (1)
 

 

or T² = 4*pi²*(0.357 kg/10.0 N/m). 

This leads to T_{TH_BEST} = 1.18717 seconds, where the underlined 8 indicates there are only three sig. figs.  Now we have  a "benchmark" 
for the experimental value of T which I am about to compute; see below. 

Before we address the direct measurement of T , let's find the uncertainty in the theoretical value ΔT_TH    given by formula under (Q-2):

(1.18717)*( 1.3333/714.700     +     0.03125/20.0) = (1.18717)*( 0.000186554     +     0.0015625) = (1.18717)*( 0.00342804)  = 0.0040697  = 0.004  if rounded down to one sig. fig.  

If you  use the more accurate condition of 0.025 g for the uncertainty, we get:  

(1.18717)*( 0.0333/714.700     +     0.03125/20.0) = (1.18717)*( 0.00004663865546     +     0.0015625) = (1.18717)*( 0.001609138655) = 0.001910321138 = 0.002 if rounded down to one sig. fig.  

These errors seem inconsistent with the precision of the reported average  T_{TH_BEST} = 1.18717 seconds, which is precise only to the 1/100 th place.  It is impossible for the third decimal place (1/1000th place) in the uncertainty to be meaningful (as in  0.004 or 0.002)  when the average period T_{TH_BEST}  is precise to only the 1/100th place.  Thus,  one might conclude that the error is "zero."

n	time for n cycles  (s)	TEX = t/n   (s)
10	11.7061	1.17061
10	11.7823	1.17823
10	11.6224	1.16224
10	12.1926	1.21926
10	11.7945	1.17945
	TEX_BEST =	1.181958 = average
	R/N=	(1.21926-1.16224)/5 = 0.011404
	ΔT inst =	0.0001/10 = 0.00001
	ΔT =	0.011404 = 0.01 if rounded to one sig.fig.

Note that in this case, since the uncertainty is 0.01 s  rounded to the 1/100th place and the average period is precise to the 1/100,000th place, then 
you would report the answer by rounding down the average to the same place: T_EX = 1.18 (s) +/-0.01 (s). Note that this is very different from the previous  example where the precision of the average ("best") was less than that of the  uncertainty,  in which case the uncertainty is taken as "zero."  

(Q-6)

Now check the discrepancy. |T_EX – T_TH| < 2(ΔT_EX + ΔT_TH),

| 1.181958 - 1.18717 | < 2*| 0.011404 + 0| = 0.022808

Now, the left hand side is zero since 1.181958  - 1.18717 = - 0.005213 = 0. Thus we can conclude that the theoretical  period equals the measured experimental period.