| QUIZ 2 (ANSWERS) | |
| READ ALL EXAMPLES. SOME PROBLEMS ARE JUST LIKE AN EXAMPLE---SEE EXAMPLE 2.9 AND #66. | |
| CH. 2 acceleration problems without Free Fall ( Part I) | |
| CH. 2 - Multiple choice 1,2,3,7,12,13, and exercise/problems 1*,2*,8*,15*,20*,67*,25*,26*,37*,38*,40*,76*,80* ,66*,68* | |
| * DISCUSSIONS PROVIDED. | |
| SELECTED DISCUSSIONS TO exercises/problems
BELOW. ALL PROBLEMS ARE DUE EVEN THE ONES WITHOUT DISCUSSIONS, WHICH ARE DESIGNED TO HELP YOU DO RELATED PROBLEMS. |
|
| 1. I WOULD EXPECT YOU TO BE ABLE TO DO THIS
PROBLEM WITHOUT MUCH EFFORT: HERE'S A HINT: (a) THE ANT'S POSITION AT A IS NEGATIVE, AND AT C AND B, POSITIVE. (b) The displacement may be negative or positive. For example in the case of B to C, displacement is -30 cm. |
|
| 2. (a) Displacement , as opposed to
distance discussed in detail #80 below, is defined to be xf
- xi. Here f means final and i means
initial. Compute the difference for each requested time
interval. For example, between 1.0 s and 10.0 s, the displacement
is 6 m - 1 m. (b) FOR DISTANCE you must find the ABSOLUTE VALUE of each displacement. Note the displacement can be positive or negative, but distance is always positive, so you must find the absolute value Below is another way of seeing the problem: Solve: (a)
The displacement is
(b) (i)
|
|
| 8. In each case recall the slope of x is
the velocity vx. (a) The slope
constant and greater than zero. (b) slope is zero (c) slope is
negative and less than zero. Below is another way of seeing the problem:
Solve: The
graphs of
|
|
| 15. (a) See example 2.12. The relative
speed is given by the ratio of the truck length and the time to
pass. Since you are going faster than the truck and in the same
direction, subtract the relative speed from your speed to
get truck's speed relative to road. (b) distance = speed * time, where you are using speed relative to the road and time to pass. |
|
| 20. (A) the slope of constant; find rise/
run (B) same slope as previous part. (C) the slope is zero (D) slope is
constant and negative; find rise/run (E) same slope as previous
part (F) same slope as previous part (G) the slope of the tangent
is zero Below is another way of seeing the problem: 2.20. Set
Up: The instantaneous velocity at any point is the
slope of the x versus t graph at that point. Estimate the slope from the graph. Solve: A:
Reflect: The
sign of
|
|
| 67. Average speed = total distance
/total time, where total time = 10 mi/8 mi/h + 10 mi/V and V is
the average speed on the last half of the trip. We have total
average speed = 20 mi/( 10/8 h + 10/V) . For each part
set total average speed to the listed value and solve the previous
equation for V. (a) total average speed = 4 mi/h. (b) total average speed = 12 mi/h. (c) total average speed = 16 mi/h. V must be a positive number; otherwise there is no solution. |
|
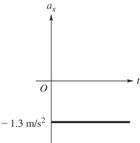
| 25. In all cases remember the acceleration is the slope of the velocity. (a) slope is positive and constant (b) slope is positive and increasing (c) slope is negative and constant. (d) slope is positive and decreasing with time. | |
| 26. (a) read from the graph (b)
acceleration = slope of velocity (c) see 25 (c). Below is another way of seeing the problem: The acceleration
Solve: (a)
Reading from the graph, at
(b)
(c) The graph of
|
|
| 37. See discussions for # 76. For part (c) compute the distance 20 m/s traffic moves for the time period easily computed in part (b). To do this problem select from the set of equations 2.8 to 2.14. | |
| 38. Below is another way of seeing the
problem:
Solve: (a)
For the motion after the brakes are applied,
The total distance is
(b)
|
|
|
40.
Below is another way of seeing the problem: Set
Up: Let
Solve:
In the next 70.0 s,
The total distance traveled is
|
|
| 66. SEE EXAMPLE 2.9 ! The equation
for the truck is x = (15 m/s)*t and for the car x = (1/2)*(2.5 m/s2)*t2.
When the car overtakes the truck the two values of x are equal, so set
the expressions equal to each other and find t, then find x. You
can find the velocity of the car when it it overtakes the truck by using
equation 2.8. Below is another way of seeing the problem: Set
Up: At
Solve: (a)
Apply
(b)
|
|
| 76. You want the ramp to be long
enough for less powerful cars and for cars with bald tires.
These are you standards from which road specs are found. #Find the acceleration of the less powerful car using equation 2.8 AND 60 MPH. Then use equation 2.13 to find the ramp length by setting the final velocity equal to 70 mph assuming the car starts from rest. # Find the acceleration of the car with bald tires using equation 2.8 AND 60 MPH. Your acceleration will be negative assuming the car moves in the positive direction when braking Then use equation 2.13 to find the ramp length assuming the car starts at 70 mph and finally comes to rest.. Below is another way of seeing the problem: Set Up: Take
Solve: on-ramp
(speeding up):
Then
This is the required length of the on-ramp. off-ramp
(slowing down):
Then
This is the required length of the off-ramp. |
|
| 68. Find the time it takes to run 10,000 m
at 2.5 m/s, then subtract 15 minutes from your answer. With
the shorter time period you computed, finally find the speed of yourself
if you run 10,000 m. Below is another way of seeing the problem: .
Set Up: Both you and your
friend run at a steady pace over the 10 km race so the equation
Solve: The
time your friend takes to complete the race is
|
|
| 80. (a) The mouse is to the right of the origin wherever the value of x is greater than zero. (b) Find the slope of the first straight line segment defined between 0 and 3 seconds. (c) Wherever the shape of the x- graph is a straight line, the acceleration is zero since the velocity is constant on those line segments . Does the x- graph ever become curved instead of straight? If so, the acceleration has become non zero. The x-graph seems to be a mixture of straight line segments and curves so the acceleration seems to change during the entire trip (d) The maximum speed is given by the section of the graph with the largest magnitude of slope---either the slope of a straight line segment OR the slope of the tangent to the graph. Where does this occur? (e) If the mouse moves rightward, the slope is positive. Otherwise it moves either leftward (if there is a negative slope) or does not move (wherever the slope is zero.) (f) Observe the graph. To get the distance you must always add since distance is always positive. In the first 3 seconds for example, the mouse moves 40 cm. For the entire 10 seconds, you must find the individual distances for EACH time period AND ADD THEM UP. Hints: Here are helpful time periods: 0 to 3, 3 to 5, 5 to 7 and 7 to 10 seconds. LOOK AT EACH TIME INTERVAL AND FIND THE DISTANCE FOR EACH FROM THE GRAPH, THEN ADD THEM UP. (g) The mouse speeds up whenever the slope seems to get steeper. Look at the curved sections of the graph or wherever the slope changes. (h) Those equations apply wherever the curve is a straight line segment or is parabolic. Below is another way of seeing the problem: : The
velocity is the slope of the x
versus t graph. The sign of
the slope specifies the direction of the velocity. Solve: (a)
The mouse is to the right of the origin when x
is positive. This is for
(b)
At
(c) The acceleration is not
constant. For constant a the x-t
graph would be a section of a parabola, and it is not. (d) The speed is greatest
when the magnitude of the slope is greatest, and this is between 5.0 s
and 6.0 s. The speed in this interval is
During this part of the motion the velocity is
negative and the mouse is moving to the left. (e) The mouse is moving to
the right when x is
increasing. This happens for
(f) In the first 3 seconds
the mouse travels from 0 to 40.0 cm so it travels 40.0 cm. In the first
10 seconds the mouse travels from 0 cm to 40.0 cm, from 40.0 cm to
(g) The mouse is speeding
up when the slope of x versus t
is increasing. This happens at 5.0 s and between 7.0 s and 8.5 s. The
mouse is slowing down at 3.0 s, between 6.0 s and 7.0 s and between 8.5
s and 10.0 s. (h) No, the acceleration is
not constant during this entire interval and these formulas apply only
for constant acceleration. |
|