| QUIZ 4 (ANSWERS) |
| NOTES |
| SAMPLE TEST 2 |
| READ ALL EXAMPLES. SOME PROBLEMS ARE JUST LIKE AN EXAMPLE. |
| CH. 3 CIRCULAR MOTION AND 2D RELATIVE MOTION; CH. 4 ~ NEWTON'S LAWS |
| CH. 3 - CONCEPTUAL QUESTION: 8 Multiple choice 11, 12, 17 and exercise/problems 31, 34, 38, 39, 40 |
| CH. 4 - Multiple choice 5, 11, 16, exercises/problems 6, 8, 23, 24, 25, 28, 29, 31, 32, 33, 35, 36, 37, 48, 49, 50 |
| * DISCUSSIONS PROVIDED. |
| TURN IN :CH. 3~ 38, 40, CH. 4~ 8, 23, 33, 36 (TRY #35) , 48, 50 (TRY #49) |
| ERROR LOG 1; NOTE CORRECTION TO #40 (C) |
| SELECTED DISCUSSIONS TO exercises/problems
will be or are posted BELOW.
ALL PROBLEMS ARE DUE EVEN THE ONES WITHOUT DISCUSSIONS, WHICH ARE DESIGNED TO HELP YOU DO RELATED EXERCISES. |
| CHAPTER 3 |
| 38. At the point shown on diagram, the
airplane is not yet traveling in a circular path but will be when it
reaches the bottom of the dip. | centripetal acceleration| = aR = V2/R, where V is the speed. At the bottom the vector points upward vertically. Find the range of speed V such that the |centripetal acceleration | is less than 5.5g. Above that level. the force of the interior of the airplane on the pilot will be so large as to cause internal injuries. More in a later chapter (Ch. 6). |
| 40. See discussion related to figure
3.29, example 3.10 and example 3.11. (a) Tan theta = (2.0 m/s) / (4.2 m/s) = 1/2.1. Find the magnitude of the angle of the net vector makes with East direction. The direction is South of East. The magnitude V of the net vector may be obtained using the Pythagorean Theorem: V2 = 2.02 + 4.22 . (b) time = width of river/4.2 m/s (c) distance = (2.0 m/s)*time |
| CHAPTER 4 |
| 8. sum of forces in x direction = pos - neg m*ax = 0 - fk since there is no force in the positive x direction. Thus: magnitude of friction force = fk = - m*ax > 0, since the acceleration is negative. Compute the acceleration ax from the kinematic information and find the magnitude of the friction force. |
| 23. (a) m*ax = 0 - fk
since there is no force in the positive x direction. ax = - fk /m. Note the acceleration is negative and fk is 25 % of the car's weight. (b) Go back to Ch. 2 and use equation (2.13) and solve for the displacement when the final velocity is zero and the initial velocity is given. |
| 33. See lecture example 5.10, which includes a nice picture of the forces on a box being dragged by a man. |
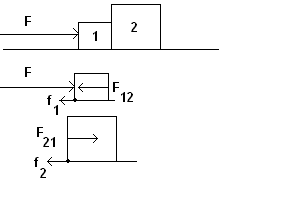
| 36. A force of magnitude F
is applied to the left box, box 1. We do not show the vertical vertical forces which cancel out. We will discuss the vertical forces in class. See the figures below that show the entire system followed by the isolated boxes and let rightward be positive. BOX 1: sum of forces in x direction = pos - neg m1*ax = F - f1 - F12, where F12 is the magnitude of the contact force on 1 from 2. BOX 2: sum of forces in x direction = pos - neg m2*ax = F21 - f2, where F21 is the magnitude of the contact force on 2 from 1. Note F21=
F12 = Fc = magnitude of the
contact force between the boxes. Add these two equations to cancel the contact force magnitude Fc,
and find the acceleration in the x direction. Note the magnitudes of the
friction forces are given as f1 and f2
and are not necessarily equal. |
| 48. (a) Sum of forces in x direction = pos -
neg m*ax = F - 0 = F = magnitude of force of gun on bullet since there is NO friction. (b) See class notes and examples in book. (c) Divide the acceleration above by g = 9.8 m/s2. (d) Ch. 2 methods. |
| 50. (a) In both cases the craft moves down.
In one case the craft slows down, do the acceleration is up. In
the other case the craft speeds up as it moves down, so the acceleration
is down. (c) Let down be positive. If slowing down we have ma = pos - neg = mg' - 25000 N, where a = -1.20 m/s2. If speeding up we have ma = pos - neg = mg' - 10000 N, where a = +0.80 m/s2. Solve these two equations for for the mass m and for g', the gravitational acceleration on Planet X. |