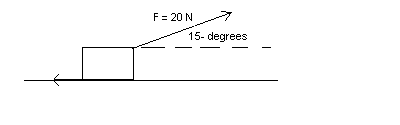|
|
|
From Autumn 99! |
|
|
|
From Autumn 99! |
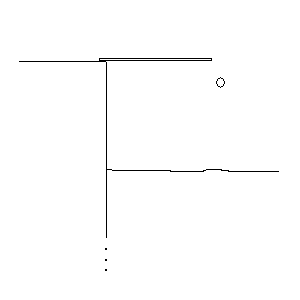
1. (20 points) A ball is dropped toward a lake from a diving board that is 11 m above the surface of the water. After the ball hits the water, it sinks downward with an upward acceleration of 3.0 m/s2 .
What is the maximum depth reached by ball below the water?
| Solution Outline: First find the velocity when it
hits the water. That's easy. V22 = V12 - 2g(Y2 - Y1)= V22 = V12 - 2g(-11 m). Note: V2 = velocity when it hits the water. Note that you should take the negative square root!! Note also that V1 = 0. Thus, V2 = -14.68 m/s. Note that Y2 - Y1 = -11 m is negative because the ball moves down! Note: acceleration = -g is negative in the air. The next part is a little tricky , but not excessively so. You really just have to be careful that's all. We assume that in the water the acceleration is directed upward and therefore is positive. Thus, a = +3.0 m/s2. Now write the equation: V32 = V22 +2a(Y3 - Y2). Note that V2 = - 14.68 m/s. Set V3 =0 because the ball stops when it reaches the maximum depth. (At this point it stops and turns around and begins to rise back to the top!) Thus, 0 = V22 +2a(Y3 - Y2). Solve for Y3 - Y2 using the fact that V2 = -14.6 m/s. Note that Y3 - Y2 is negative because the ball is moving in the negative direction, which is down.. Take the absolute value of the answer to get the depth. |
2. (20 points)
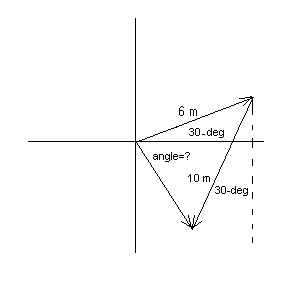
A child starts from the front door of her playhouse and follows the route shown in the above figure. Her first displacement has magnitude 6 m and her second displacement has magnitude 10 m.
(a) (10 points) What is the magnitude of the resultant displacement?(b) (10 points) What is the value of the reference angle that the displacement makes with the x-axis?
| Solution Outline: (a) Note that the second displacement vector with magnitude = 10 m makes an angle of 60 degrees with the horizontal because it makes an angle of 30 degrees with the vertical!! Think about it. Thus the components of the resultant vector are: Cx = 6cos30 -10cos60 Cy = 6sin30 -10sin60 You get the magnitude by evaluating Cx2 + Cy2 and taking the square root. (b) Note that the resultant vector lies in the 4th quadrant. The reference angle is given by Tan-1(|Cy|/|Cx|). Note we are taking the ratio of the absolute values. |
3. ( 20 points) A place kicker must kick a football from a point 37-m from the goal. The ball must pass over (clear) the crossbar, which is 8.0 m high. When kicked, the ball leaves the ground with a speed 20 m/s at an angle of 50–degrees with the horizontal.
(a) (2 points) Does the ball pass over (clear) the crossbar ? Answer yes or no. If the answer is yes, what is the height of the ball above the top of the crossbar. If the answer is no, what is the distance of the ball below the top of the cross bar?| Solution Outline: See problem 20, Ch. 3
from Quiz 2. (a) First find the time t1 = 37 m/Vx . Note that Vx = 20 cos50o . Then find the vertical height: y1 - yo = 20 sin 500 t1 - ˝ gt12. Check to see whether this result is greater than or less than 8.0 m and by how much. (b) Vy = 20 sin 50 - gt1 and Vx = 20 cos50o . Evaluate Vx2 + Vy2 and take the square root to find the speed. |
4. (20 points) A 2.0 kg block is connected a 6.0 kg block by a light string over a frictionless pulley. No friction in the problem! The masses are allowed to move over a fixed wedge with a horizontal section and an inclined section that makes an angle of 30 degrees with the horizontal. An applied force of magnitude F = 200 N pulls the 2.0- kg as shown. The 6.0-kg mass moves up the incline and thus the 2.0-kg mass moves to the left.
(a) (15 points) What is the acceleration a of the blocks?(b) (5 points) What is the tension T in the string ?
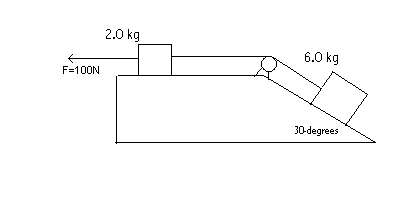
| Solution Outline: (a) For the block of mass m = 2.0 kg we have: ma = pos - neg = F - T Ma = pos - neg = T - Mgsin30 |
5. EXTRA CREDIT. A 1.00-kg particle is under the influence of a force of magnitude F = 20.0 N over a distance 5.0 m. The coefficient of kinetic friction is .010. If the box starts from rest, what is the speed of the box after is moves a horizontal distance 5.00 m?