FALL '11 TEST 3 SOLUTIONS
From Autumn 99	Solutions to Real Test 2

1. (20 points) Ch. 5

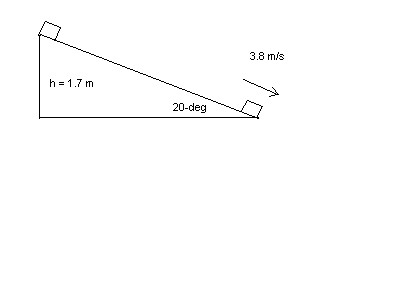
A 2.10 x 10³ kg box starts from rest at the top of a long drive way of length L from a vertical height h = 1.7 m. The driveway makes an angle of 20-degrees with the horizontal. At the bottom of the hill, the speed of the box is 3.8 m/s.

Please use the conservation of energy methods of Ch. 5 in the presence of friction.

What is the coefficient of kinetic friction between the block and the incline?

Solution Outline:

K₁ + U₁ = K₂ + U₂ + Heat
0 + mgh = ½ mv₂²+ 0 +µmgcos20*L
0 + mgh = ½ mv₂²+ 0 +µmgcos20*h/sin20

Note that L =h/sin20 since h = Lsin20

Solve for µ.

2. (20 points) Ch. 6

A billiard ball (of mass m) rolling across a table at 1.50 m/s makes an elastic head on collision with an identical ball. (of the same mass m!).

(a) (16 points) Find the velocity of each ball if the second ball is moving toward the
first at a speed of 1.00 m/s.

(b) (2 points) What is the direction of motion of the first ball after the collision, to
the right or left?

Solution outline:

Note that the masses cancel, so
v_1i + v_2i =   v_1f + v_2f or
1.5 - 1 = v_1f + v_2fThus,
0.5 = v_1f + v_{2f

Also,} v_1i - v_2i = - (v_1f - v_2f ) or
1.5 - (-1) = - (v_1f - v_2f )
Thus,
2.5 = - (v_1f - v_2f )

Note that v_1i = 1.5 m/s and v_2i = -1.0 m/s
Solve the two equations in bold above for the final velocity of each block. Note if the velocity is negative, then the object moves left.
Answers: v_1f = - 1.0 m/s and v_2f = +1.5 m/s

3. (20 points) Ch. 6

A 15.0 g bullet with initial speed 270 m/s (just before the collision) is fired into a 80-g wooden block that is initially at rest on a horizontal frictionless surface and is connected to a spring of spring constant k. The bullet sticks inside the block after the collision.

Suppose that the spring compresses a maximum distance 0.75 m after the collision.

What is k?

For a diagram, see this:

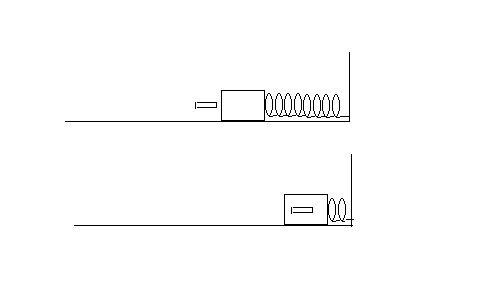
Solution outline:
m = 0.015 kg , M = 0.080 kg , V = 270 m/s and x = 0.75 m.
First use conservation of momentum:

^{mV = (m + M)V}f

Solve for V_f

Then use conservation of energy:

½(m + M)V_f² = ½kx² . Solve for k

4. (20 points) Ch. 7

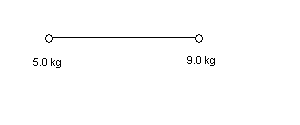
Two masses are shown below on a line, separated by a distance of 12.0 m. The mass values are indicated in the diagram. Find the distance from the left mass at which an object can be placed so that the net gravitational force is zero.

Solution outline: Please see problem 34 just like this in
Quiz 6. Same problem, different numbers.

5. Credit (8 points) Ch. 8

The beam below has mass 25 kg. Find the tension T in the cable.

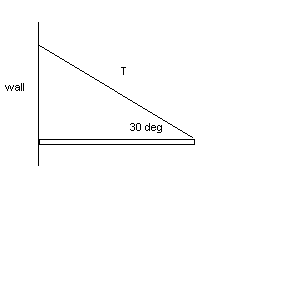
Solution outline: This problem could appear on the test as extra credit on the test Monday as extra credit only. However, you should also study the other problems you are working on in Ch. 8 as possible extra credit problems. Please see the example in the book. This problem is easier because there is no extra mass in the form of a person standing on the beam to complicate matters.

Find the tension in the cable. Take torques on the beam about the axis at the left end of the beam attached to the wall.

Sum of the torques = 0 = pos - neg

0 = torque of tension - torque of beam mass

0 = T*Lsin30 - mg*L/2 ,
where L = beam length. Note that the beam mass acts at the center of the beam. That's why we use L/2. Read the section on center of gravity in the textbook!

Solve for T = mg/2*sin30