From Autumn 99

Real T3 Answers

1. (20 points)

 

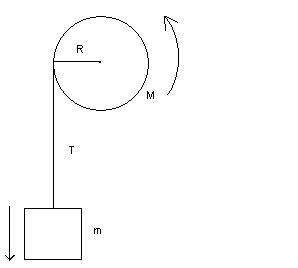
A solid cylindrical pulley of mass M = 5.50 kg and radius R = 0.660 m is used to lower a bucket of mass m = 3.10 kg into a well. See the schematic of the system below.

  1. (5 points) What is the tension T in the string?
  2. (5 points) What is the linear acceleration of the bucket?
  3. (5 points) What is the angular acceleration of the cylinder?
  4. (5 points) Suppose the bucket starts from rest and falls for 4.00 seconds.
    How far does it drop?

 

Solution Outline: This problem is so easy, I am almost tempted not to post a solution. (I say this with a SMILE !
)

The only thing you need is a review of the concept of Newton's 2nd law of rotations, which says that

This is just like
F = ma.
Thus,

TR= I(a/R) since

Note that I = ½ MR2
The next equation is:

ma = mg - T

(a) and (b) Solve these two equations for T and a !
(c)

(d) y = (½)at2

 

2. (20 points)

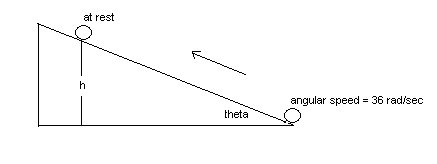
A sphere of mass m = 24 kg and radius R = 0.20 m rolls without slipping up a ramp that is inclined at an angle with the horizontal. A schematic of the system is shown on the diagram below. Suppose that the angular speed at the bottom of the hill is 36 rad/sec.

What is the vertical height h that the sphere reaches before momentarily coming to rest?

Hint: Use conservation of energy in the presence of rolling!
The moment of inertia of the sphere is I =
.

Solution Outline:  Guess what ?
See Test 2 Problem 4 for extra credit!!
I will copy those solutions and post them here. It is as easy as that !
The only difference is that in this problem, the ball starts at the bottom and ends at the top!!
Use conservation of energy,
K1 + U1 = K2 + U2
(1/2)mv2 + KROT + 0 = 0 + mgh,           where KROT  = ½ I w2 =  ½(2/5*mR2)w2
 (1/2)mw2 R2 + ½(2/5*mR2)w2 = mgh

Solve for h.

 

3. (20 points)

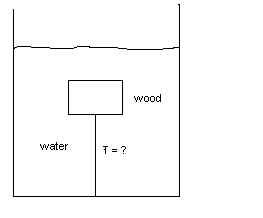
A 5.00-kg block of wood (density 635 kg/m3 ) is connected to a light string that is connected to the bottom of a large beaker filled with water. Assume the density of water is 1000 kg/m3. A diagram of the system is below.

What is the tension T in the string?


Solution Outline:  Guess what ?
This problem is almost just like that quiz problem with the spring under water. Same concepts. Click to the hints to the problem here  and scroll down to #24.

Solve for T. Note that you  have to find the volume V from the relationship that:
V = m/635 kg/m3
For extra credit, would the tension  T be greater or less if the system was on the moon?


4. (20 points)

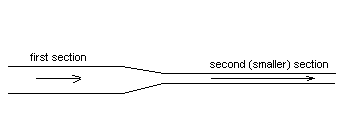
A liquid () flows through two horizontal sections of tubing joined end to end. In the first section the crossectional area is A1 = 9.5 cm2 , the fluid speed is 265 cm/s and the pressure is P1 = 1.2x105 N/m2. In the second section the crossectional area is A2 =  9.0 cm2.

Find the pressure P2 in the second (smaller) section.

 

 


Note: v2 = A1·v1/ A2

You know v1. Find v2 from the above equation and solve for P2 from the equation below. Note that y1 = y2 and so they cancel !:

wpe1.jpg (5117 bytes)


5. Extra Credit

An automobile fuel tank has volume =12.000 gallons. It is filled with 11.125 gallons of gasoline when the temperature is 100C . The vehicle is left in the sun and the temperature rises to 350C. The expansion coefficient for gas is 9.6x10-4 (oC)-1

Does any gas overflow from the tank? Answer yes or no and prove your answer!