|
From Spring 2000 |
Test 1 Spring 2001 Test 1 Spring 2002 |
1.(20 points)
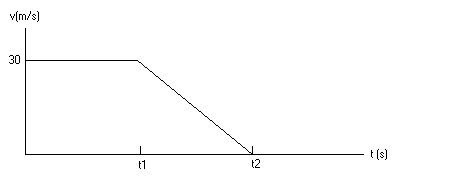
A driver is traveling on a country road at constant velocity +30 m/s. He spots a piece of junk in the middle of the road at time t = 0. After a certain reaction time t1, the driver applies the brakes and decelerates with acceleration -5.0 m/s2 until the car comes to rest at time t2. (V2 = 0). At time t1, the displacement is 100 m. A diagram of the motion is shown below.

(a) (8 points) What is t1 ?
(b) (12 points) What is the average velocity for the entire motion?
| Solution: (a) 100 m = v1·t1. Thus t1 = 3.3 sec (b)VAV = total displacement/total time. We need t2 - t1 and x2 - x1. Note that we already know x1 - x0 = 100 m and t1 - t0 = t1 = 3.3 sec. Let's get the time first : t2 - t1 = (v2 - v1)/a = (0 - 30m/s)/(-5m/s2) = 6 sec. Thus, total time = 3.3 + 6=9.3 sec. Now we need the total distance; Let's get x2 - x1. There are a few ways to do this: Way1: x2 - x1 = (v2 + v1)·(t2 - t1)/2 = (O + 30)·6/2 = 90 m Way2: x2 - x1 = v1·(t2 - t1) - ½5·(t2 - t1)2 =30·6 - 2.5·36= 90m Way3: v22 = v12 - 2·5·(x2 - x1). Thus, (x2 - x1) = (30)2/10= 90m (Can you think of a 4th way?) Anyway, VAV = (100 + 90)/ 9.3 = 20.4 m/s |
2. ( 20 points) The 3 vectors are oriented as shown in the figure below.
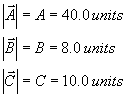
Both the vector-A and the vector-B have related angles of 45 degrees with the x-axis.
Find:
(a) (7 points) the x and y components Rx and Ry of the resultant vector given by:
![]()
(b) (6 points) The magnitude.
(c) (7 points) The direction of the resultant vector. What is the related angle with the x-axis? In what quadrant does the resultant vector point? Make a sketch of the resultant on the axes provided. Show the related angle in the sketch.
| Solution: (a) Rx = -8cos45 - 40cos45 + 10 cos 90 = -8cos45 - 40cos45 Ry = +8sin45 - 40sin45 + 10 sin 90 = +8sin45 - 40sin45 + 10 (b) (c) Since Rx <0 and Ry < 0 the vector points in quadrant 3. To get the reference angle, use: Tan øR =|Ry|/|Rx|. |
3. (26 points)
A parachutist bails out of a plane with initial speed zero and falls downward for a distance of 50 m. Then the parachute opens, and she decelerates (slows down) with an acceleration of magnitude 2.0 m/s2 . She reaches the ground with a speed of magnitude |V3 |= 3.0 m/s. A schematic of the motion is shown below. (Distances are not necessarily to scale.)
Note that before the parachute opens, the acceleration points downward with magnitude g, and after the parachute opens, the acceleration points upwards with magnitude
2.0 m/s2 .
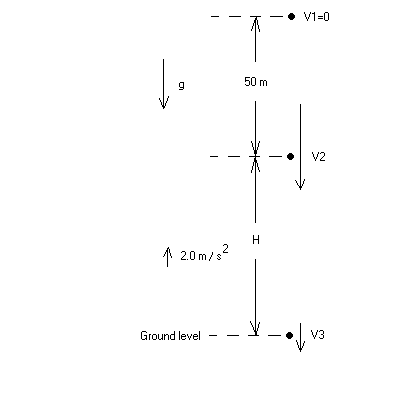
(a) (10 points) What is the distance H that she falls with the chute open?
(b) (10 points) What is the total time that she is in the air?
(c) (6 points) What is the average velocity for the entire trip?
| Solution: (a) Let down be positive. Easiest way to get the distance is to use: v32 = v22 + 2(-2)(y3 - y2). Note that down is positive means that up is negative in this case. That is why the acceleration is negative: (y3 - y2) = (v32 - v22)/(-4). v3 is given. It would help if we knew v2. How do I get that? One way is to use: v22 = v12 + 2g(y1 - y2) = 0 + 2g·50 Plug this into : (y3 - y2) = (v32 - v22)/(-4). and get (y3 - y2) = H. (b) We need: (t2 - t1)+(t3 - t2) = total time Find (t2 - t1): 50 = v1·(t2 - t1)+ ½·g· (t2 - t1)2= 0 +½·g· (t2 - t1)2 Solve for (t2 - t1). Find (t3 - t2): Use (y3 - y2) = (v2 + v3)·(t3 - t2)/2 Solve for (t3 - t2). Remember that you know v3 and v2. You can also use: (t3 - t2)=(v3 - v2)/(-2m/s2) (c)VAV = total displacement/total time. You know the total displacement since you know H and you can evaluate H + 50 m. You know the total time from part (b). Find VAV |
4.(20 points)
A handball player stands 50.0 m away from a wall and throws a ball as shown schematically below. The initial speed of the ball is v0 = 40.0 m/s and the initial angle is 30.0 degrees with respect to the horizontal.

| Solution: This problem is just like problem 20, Ch. 4, Quiz 4. Please refer to the hints posted on this web site. (a) t =50 /V0cos 30 Vy = V0sin30 - gt Vx = V0cos30. Plug Vx and Vy into the formula for the speed ! (b) See hints to Q4. (c) Rising if Vy >0. Otherwise, it is falling.... |
5. (26 points)
The two blocks below are connected by a string that is wrapped around a pulley at the top of the double inclined plane shown. The masses are given by m1 = 20.0 kg and
m2 = 2.0 kg . The coefficient of kinetic friction between the blocks and both surfaces is 0.10. The system is accelerating and speeding up.
(a) (18 points) What is the magnitude of the acceleration a of the blocks?
(b) (8 points) What is the tension T in the string?
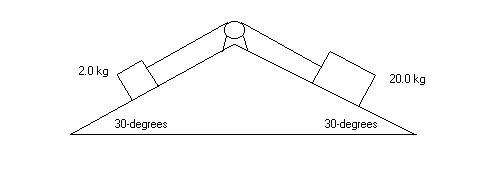
| (a) m1a = m1gsin30 - T- (0.10)m1gcos30 m2a = T - m2gsin30 - (0.10)m2gcos30. Solve for a by adding to cancel T. (b) Solve for T by plugging a into either of the original equations. |