|
From Spring 99 |
1. (20 points)
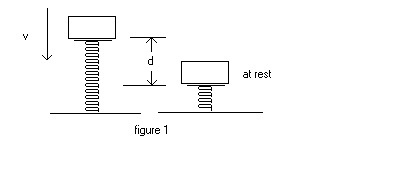
A 2.0- kg block is dropped from a certain height above a spring of spring constant k = 1900 N/m that is in its relaxed position. Just before the block strikes the spring, it has speed v. See figure 1. The spring is then compressed a maximum distance d = 0.10 m before the block comes momentarily to rest.
(a) ( 15 points) What is the speed v of the block just before the block strikes the spring?See figure 1.
(b) (5 points) From what height h above the spring was the block dropped? See figure 2.

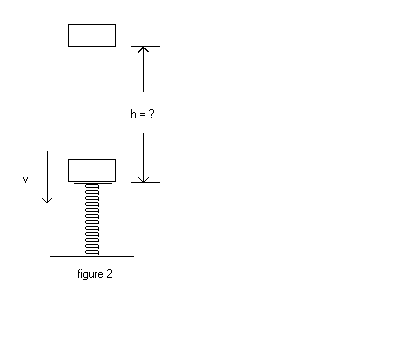
| Ch. 8. Solution: (a) ½mv2 + mgd = ½kd2....Find v ...Guess what? No quadratic!!! Sorry about that. (b) mg(h + d) = ½mv2 + mgd.....Notice how the mgd cancels from both sides of the equation so that we get: mgh = ½mv2...Find h.. Note that you should keep checking below for the other solutions, which will be appearing every half hour or so until all answers are posted..... |
2. (20 points)
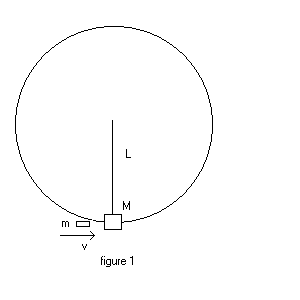
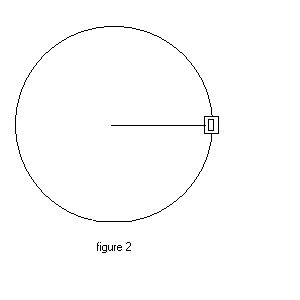
A bullet of mass m = 50.0 g (grams) and speed v is fired into a pendulum bob of mass M = 1.00 kg (kilograms) and sticks inside . See figure 1. The entire system swings so that the rod is in a horizontal position before momentarily coming to rest. See figure 2. The stiff rod suspending the bob has length L = 2.00 m and negligible mass.
What was the speed v of the bullet before the collision?
| Solution: Ch. 9 Part 1 is for a closed system of bob and bullet......gravity
does not act for the moment just before and after the collision.....so
that Part 2 has the presence of the Earth which acts on the bullet and the
bob through the force of gravity, so the system of bob and bullet is no
longer closed!! We've got to use conservation of energy, since momentum
is not conserved for an open system.. Solve the two above equations for v... |
3. (20 points)
Consider a frictionless track ABC as shown below. A block of mass m1 = 5.00 kg and speed 12 m/s collides with a block of mass m2 = 1.00 kg at rest at point B. The collision is elastic.
(a) (3 points) Calculate the maximum height to which m2 rises after the collision.
(b) (3 points) Calculate the maximum height to which m1 rises after the collision.
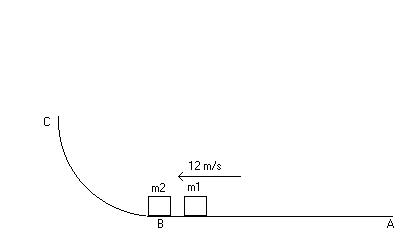
| (a) Part 1 is for a closed system just before and after the collision: Use conservation of momentum....find the velocities of each car after the collision using the two equations: m1v1i = m1v1f + m2v2f and v1i - v2i = v2f - v1f...Solve these 2 equations for elastic collisions for v1f and v2f .. Part 2: Then use conservation of energy to find how high m2 rises (open system as it rises since earth acts on the two masses through the force of gravity...): ½m2v2f2 = m2gh2 (b) use conservation of energy for the m1
to find how high it rises (open system with the presence of
earth): |
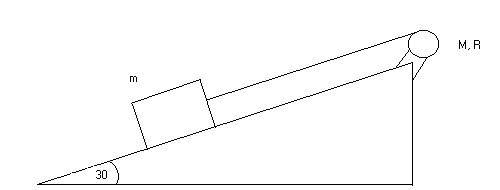
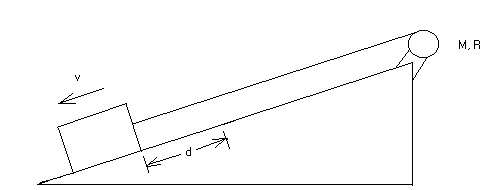
4. (20 points) A pulley in the shape of a solid cylindrical disk of radius R = 0.20 m and mass M = 10.0 kg is mounted on a frictionless horizontal axis. A massless string is wrapped around the pulley and is attached to a block of mass m = 2.0 kg that slides along a frictionless surface inclined at an angle of 30-degrees with the horizontal.
The system begins its motion from rest. After the mass m slides along the incline a distance d, the speed of the mass is v = 2.0 m/s.
(a) (12 points)Use conservation of energy to calculate d.
(b) (4 points) What is the acceleration a of the block down the incline?
(c) (4 points) What is the tension T in the string?
| Ch. 10: Solution: (a)mgh = ½mv2 + ½I(v/R)2 mgdsin30 = ½mv2 + ½I(v/R)2 where we used the relationship between angular speed and linear speed in the last term for the rotational kinetic energy...Find d. Note that I = ½MR2... (b) v2 = 2ad...find a... (c) ma = pos - neg ma = mgsin30 - T..... find T |