Sample final from Spring 2000


Ch. 8 and 9 (Extra Credit)

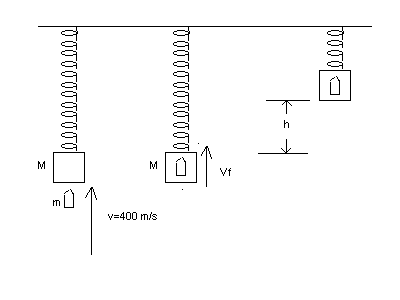
1. (20 points) A bullet of mass m = 10.0 g is fired vertically into and sticks in a block of mass M = 1.00 kg attached to a spring of spring constant k = 
20.0 N/m . Assume that the speed of the bullet just before the collision is 
400 m/s.

What is the height h that the bullet and block rise to before momentarily coming to rest?


1. Solution.
This problem is easy ! 
First use conservation of momentum to get Vf :
mv = (m + M )Vf .......find Vf = mv/(m+M)       (Note: m +M = Closed system)

Second use conservation of energy to find the distance h that  m and M  rise:
K2 + U2 = K3 + U3
½(m + M )Vf 2 + 0 = 0 + (m +M)gh + ½kh2     (Note: m + M   not a closed system since gravity and the spring force act on m and M)

Solve a quadratic for h. 

2. (12 points) Mass m1 is connected to another mass m2 by a string that is wrapped around a pulley in the shape of a solid disk of radius R = 3.0 m and mass M = 2.0 kg. Note: m1 = 5.0 kg and m2 = 2.0 kg. Assume the blocks start from rest. Initially, m1 is located a distance h above the ground. After m1 drops a distance h to the ground, the speed v of the blocks is 10.00 m/s.

What is h?


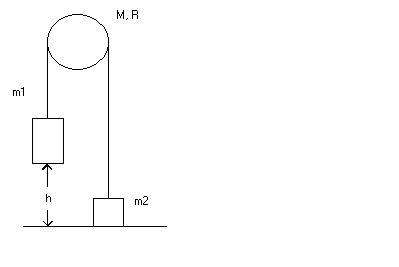
2. Solution.
Another easy problem. You're  on a roll !  Use  conservation of energy please! Let the zero of gravitational energy be on the ground level. Thus,

KA + UA = KB + UB

0 + m1gh = ½(m1 + m2)v2 + ½I·v2/R2  + m2gh.   Solve for h. 

3. (20 points)

A merry-go-round of radius R = 2.0 m has moment of inertia I = 250 kg-m2 and is rotating initially at angular speed .
Initially, a child of mass m = 25 kg is standing in the edge of the merry-go-round. She walks to a location a distance R/2 from the center.

What is the new angular speed of the merry-go-round?

 


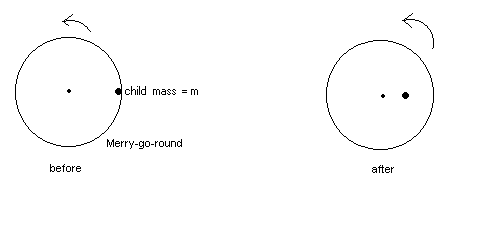
3. Solution.
This ain't hard ! Really.
L i = L f  so that 
I i wi = I f wf
(250  + mR2)wi = [250 + m(R/2)2]wf   .    Solve for wf. 

 4. (20 points)
One end of a uniform beam of mass 50-kg is attached to a wall with a hinge. A cable supports the other end. The relevant angles are shown. The beam makes an angle of 60-degrees with the vertical wall.
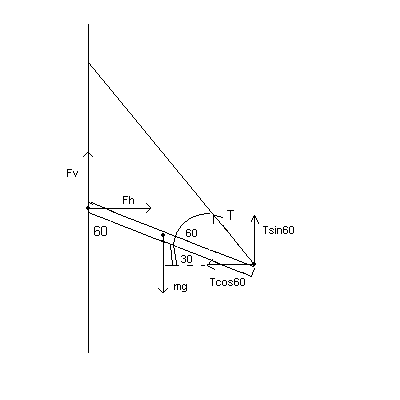
(a.) (16 points) Find the tension T in the cable.
(b.) (2 points) Find the horizontal component Fh of the force of the hinge on the beam.
(c.) (2 points) Find the vertical component Fv of the force of the hinge on the beam.



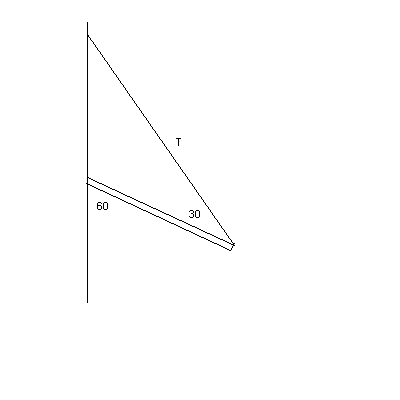
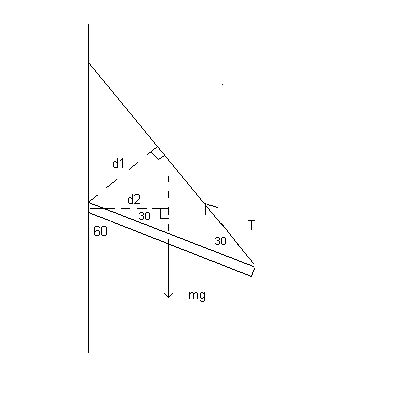
4. Solution. Not hard with a little thought. See the above diagram.
(a)To get the tension T using  the torque equation, draw a perpendicular from the axis to the line of action of the tension T.  Call this d1. Then draw another perpendicular form the axis to the line of action of mg. Call this d2. Then the torque equation is simply:

0 = d1· T  - d2· mg. 

Now from inspection , d1 = Lsin 30 and d2 = (L /2)cos30.    Solve for T.

(b) See the figure below. Fh and Fv are shown and T is broken up into  2 components. Clearly T makes angle  of 60 degrees with the horizontal, because the beam makes an angle of 60 with the vertical and an angle of 30 with the horizontal. (Since the beam makes an angle of 30 with T at the right end as shown in the first diagram above, then T makes an angle of 60 with the horizontal. Agreed ?)
Fh - Tcos60 = 0 .    Find Fh.
(c) Fv + Tsin 60 -  mg.    Find Fv.


 5. (12 points)
A simple harmonic oscillator consists of a block of mass m = 2.20 kg attached to a spring of spring constant k= 112 N/m. When t = 0, the position and the velocity of the block are:
x0 = 0.140 m and v0 = -3.500 m/s.

The position as a function of time has the form:


(a) (6 points) Find A = the amplitude of motion.

(b) (6 points) Find the phase constant .

5. Solution. Click here to see the hint to SP1 of Quiz 13. This exam problem is almost the same, except that now the initial velocity is negative ( particle moves left , say.) Therefore the phase angle will be positive this time, unlike like SP1  in which the phase angle was negative. See class notes.

 6. (20 points) A rocket is launched from the surface of the earth with speed 2.00x104 m/s. The radius of the earth is RE = 6.37x106 m. The earth's mass is M = 5.98x1024 kg. G = 6.67x10-11 N·m2 /kg2
(a) ( 10 points) Prove that the rocket does escape the earth's gravitational field.
(b) ( 10 points) What is the speed of the rocket at an infinite distance from the earth?

6. Solution. Not too easy, not too hard, just right.
(a) 2.00x104 m/s =20.0 km/s > 11.2 km/s = escape velocity. The proof for this problem would be to derive the formula for the escape velocity from the earth, then evaluate it numerically, then state that  20.0 km/s > 11.2 km/s. To see the derivation of the escape velocity , review your class notes or see section 14.8.
(b)½mv12  - GmM/RE  = ½mv22  + O  (U = 0 at infinity because of the infinite value in the denominator of the formula for the potential energy U. )
 Find v2  . 

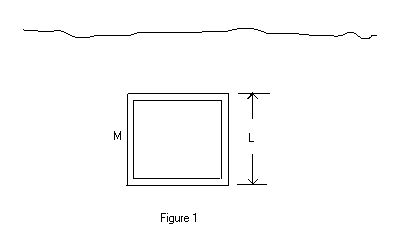
7. ( 15 points) An empty box in the shape of a cube is completely submerged under water. The exterior side of the box has length L = 1.00 m as shown in Figure 1. The mass of the box is M = 60.0 kg.
(a)(5 points) Does the box sink or rise ? Show all work to prove your answer!
(b)(5 points) What is the magnitude a of the acceleration of the box?
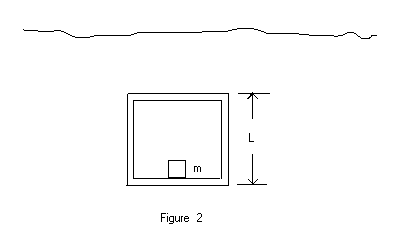
(c) (5 points) Suppose a lead block of mass m = 75.0 kg is placed inside the
empty box. See Figure 2. What is the magnitude and direction (up or down) of the acceleration of the box?



Solution:
(a) Use simple logic. Check to see if the FB is different than the weight of the box, then check to see which one is larger in magnitude... If FB is larger, then it rises...Otherwise it sinks....
FB = water density ·L3g = 1000·13 9.8 = 9800 N
Mg = 60·9.8 = 600 N approximately. 
Therefore, the box rises.
(b)
Ma = pos - neg
Ma = FB  - Mg
60a = 9800  -  588 so that a = 153 m/s2  
(c) Now check  to see if the downward weight is  greater than FB.
Mg + mg = 588 + 75·9.8 = 588 + 735 = 1323 N < 9800 N...so the box still rises, though with a smaller acceleration.
Ma = pos - neg
(M+m)a = FB  - (M + m)g
135a = 9800 - 1323  so that a = 62. 8 m/s2