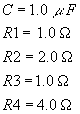Au99

Final Examination 

Solutions to Real Final!
1. ( 12 points) EXTRA CREDIT

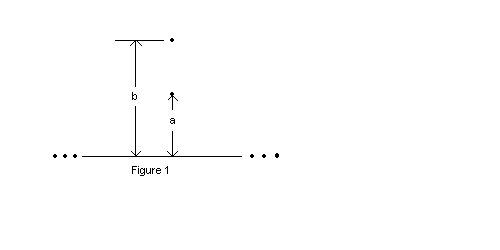
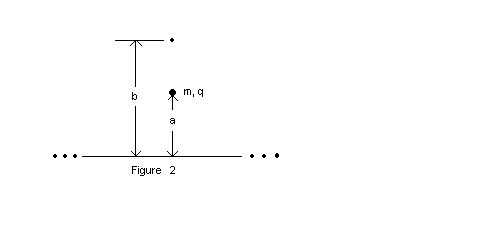
Consider a uniform line of charge of charge per unit density

See Figure 1 below.

(a)( 7 points) What is the change in electric potential between points at distances a and b from the wire, as shown. The distances are a = 4.0 cm and b = 8.0 cm.

(b) ( 5 points) Now focus your attention on Figure 2 below. Suppose a positive point particle of mass m = 1.0x10-30 kg and charge q = 2.0x10-19 C is released from rest at point a. What is the speed of the particle when it arrives at point b?

 

 
Solution:
(a)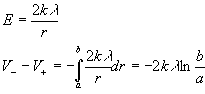

(b)

Ki + U i = Kf + Uf

0  + qVi = Kf + qVf

0 + (q)Vi - (q)Vf = Kf 

(q)(Vi - Vf)= Kf 

Solve for v
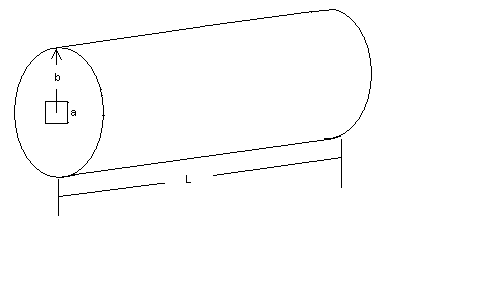
  2. (20 points)

At 200C, a heating element can deliver 500-Watts of power P. The heating element is a resistor in the shape of a hollow cylinder of length L and radius b = 2.0 mm. The hollow cavity has a square cross-section of side a = 1.0 mm. The element is made of Nichrome and thus has a resistivity

A voltage V= 100 Volts is applied between the ends of the resistor. See the figure below.

(a) (12 points) What is the length of the wire?
(b) (8 points) What power will the coil actually deliver when the temperature is raised from 200C to 12000C ? The temperature coefficient of Nichrome is given by:
0.4x10-3 (0C)-1 .

 

 

 
Solution:
(a) See the solution to real test 3. , problem 3 to find the length. Use V2/R = 500 W and solve for the length.
(b) Find the new R = R0[1 + 0.4x10-3(1200 - 20)]. Then find the new
P = V2/R. Note:  R0 is found in part (a).
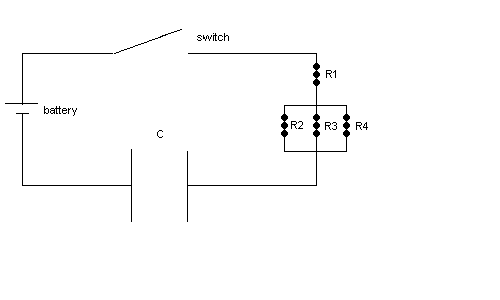
  3. ( 37 points)

The switch is closed at t = 0. The symbol C represents a parallel plate capacitor with plate area A =1.0 cm2 and a distance between the plates d = 2.0 cm. The battery voltage is 10.0 Volts. Also:

Note:

  1. (14 points) Find the charge q on the capacitor after a time period
    of 1.0x10-6 seconds.
  2. (10 points) What is the current i in R1 at t = 1.0x10-6 seconds?
  3. (8 points) What is the current i4 in R4 at t = 1.0x10-6 seconds?
  4. (5 points) What is the magnitude E of the electric field in the region
    between the parallel plates at t = 1.0x10-6 seconds?
Solution:
bulletFirst transform R3 , R3, and R4 resistors into their parallel equivalent: 
1/Rp = 1/2 + 1/1 + 1/4. Find Rp. Then add R1 + Rp = Rf.
bulletSecond, use the formula for the charge in a charging circuit given in Ch. 28. Use Rf, C and the given battery voltage in the formula. Evaluate the formula at t = 1.0 X10-6s 
bullet

Third, use the formula for the current in a charging circuit in Ch. 28.  Use Rf, C and the given battery voltage in the formula. Evaluate the formula at t = 1.0 X10-6s  to find i. This will give you the total i in the circuit.

bullet

Finally, you can find the current i4  by doing the following:
i4= iRp/4

bullet

Ed = V+ -  V-  = q/C. Use q at   1.0 X10-6s and divide by d to get E.
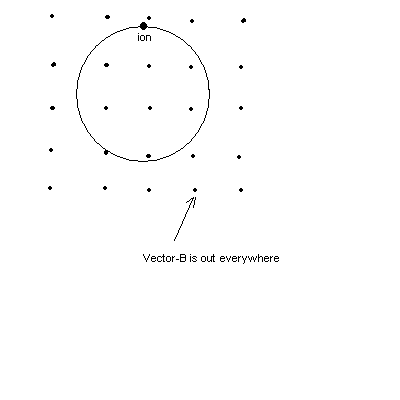
 4. (23 points)

A singly charged positive ion of charge q = 1.0x10-19 C and mass m = 1.00x10-26 kg is accelerated through a potential difference of V =1000 Volts. The ion then enters a region perpendicular to a magnetic field that has magnitude B = 1.000 T. As indicated below, in this region the magnetic field vector points outward, perpendicular to the plane of the page. The circular orbit of the particle is parallel to the plane of the page. Now focus your attention on the instantaneous position of the ion when it is at the top of the circle.

  1. (5 points) Since the ion is moving in a circle, what must be the direction of the force vector at the location of the ion at the top? Please indicate the direction of the force at that point by drawing an arrow.
  2. (10 points) What is the direction of the velocity vector at the top? Please indicate the direction of the velocity by drawing an arrow.
  3. (8 points) Calculate the radius r of the path of the ion.

 
Solution:
(a) Down, toward the center of the circle
(b) To the right, tangent to circle.
(c) Find v = speed from qV = ½mv2.  Note that
V = 1000 Volts. The find r = mv/qB
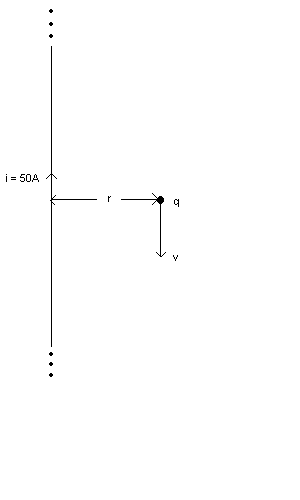
  5. ( 20 points)

A long wire has a current 50.0 A as shown in the diagram below. At a distance of r = 5.0 cm from the wire, a particle of positive charge with q = 1.0 X10-19 C moves parallel to the wire and in a direction opposite the current. The speed of the particle is v = 1.0x107 m/s.

 

  1. (10 points) What is the direction of the force on the particle due to the magnetic field of the wire? To get partial credit, you must show all work. Show the direction of the force with an arrow. Show how you got the arrow representing the force.
  2. (10 points) What is the magnitude of the force on the particle due to the magnetic field of the wire? To get partial credit, you must show all work.
Solution:
(a) Vector-B is in at the location of q. The force points right.
(b) F = qvB where,
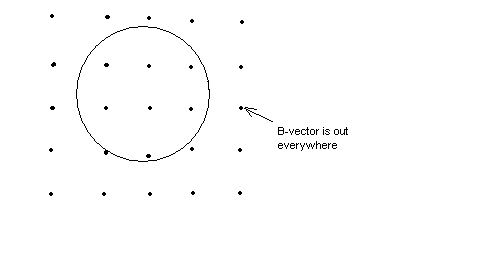
 6. (24 points)

A circular loop of wire with radius r = 1.0 m is placed in a region where a uniform magnetic field is perpendicular to the plane of the loop. The magnetic field vector points out. The magnitude of the magnetic field is allowed to vary in time according to the equation:

where t is in seconds.

Suppose the loop has a resistance R = 2.0 ohms.

 (a) ( 10 points) Find the direction of the current i in the loop, either clockwise or counterclockwise, for t > 0. Please indicate this direction by drawing an arrow at the wire.

(b) (10 points) What is the magnitude of the current i at t = 2.0 seconds?

(c) (2 points) What is the direction of the magnetic moment caused by i for t >0 ?
(d) (2 points) What is the magnitude of the magnetic moment caused by i at t = 2.0 seconds?