FINAL PART 2 SP ’12:  BELOW WE’VE NUMBERED THE STEPS TO DRAMATIZE HOW LONG THE EXAM REALLY WAS DESPITE  A FEW  PERCEPTIONS  TO THE CONTRARY. THERE WERE 26 STEPS TOTAL, NEARLY 9 STEPS PER HOUR .

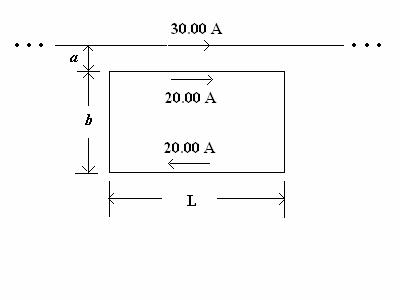
1.  (40 POINTS)

 

The long,  straight wire carries a current of 30.00 (A) and the rectangular loop carries a current of 20.00 (A). See schematic below. Both structures lie in the plane of the page. Try to use symbols in your work until the very last steps.

(a) (35 points) Calculate the net (resultant) force acting on the loop due to the long , straight wire. In other words, what is the magnitude and direction of the NET  force on the loop?   

Assume a = 1.00 cm, b = 8.00 cm and L = 30.00 cm. It may be helpful to break your solution into  parts. Explain carefully each section of your work. Indicate the direction of the net force on the loop with an arrow.

(b) (5 points)   What is the magnitude and direction of the magnetic dipole moment  of the rectangular loop? Does the loop experience  a torque due to  the magnetic field of the long wire? Answer yes or no and explain briefly. 

SOLUTIONS:

        a. Fnet = [uo*I’*I*L/(2*pi)]*[ 1/a   - 1/(a + b)], upward toward the long wire, where I’ = 20 (A),  I = 30 (A),  and L = 0.30 m; Fnet = 3.200x10 -3 N.   

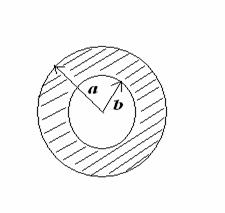
        b. magnetic moment vector is IN; NO TORQUE SINCE ANGLE  BETWEEN LOOP FIELD/magnetic moment AND LONG WIRE FIELD IS 0 DEGREES; THE FORMULA SAYS TORQUE MAGNITUDE = u*Bsin theta, WHERE u = I*area =(20.00 A)*(0.3)*(0.08)m2 = 0.480 A*m2 .

 

 

2. (40 POINTS)  

The figure below shows a cross section of a hollow,  cylindrical conductor of  radii  a and b,  carrying a uniformly distributed,  total current I.  This  problem uses symbols only. Answer in terms of r, a, b,  I and other possible constants. Radial  distance r is  measured from the cylinder’s central axis.

(a) (10 points)  What is the magnitude  B of  the magnetic field  at r = a?
(b) (4 points)    What is the magnitude B of the magnetic field at r = 2a?

(c) (16 points)   Derive the formula for the magnitude B(r ) of the magnetic field for the range  b < r < a.  Also, evaluate your formula at r = a and show your answer is the same as that of part (a). 
(d) (6 points)    What must be the  magnetic  field magnitude B at r = b/2?  Explain.

(e) (4 points)    On the axes provided, sketch the magnitude B as a function of r. Include all regions r < b, b < r < a,  and   a <  r.

SOLUTIONS:

        a.  B = uo*I*/(2*pi*a)

        b.   B = uo*I*/(4*pi*a)

        c.  B =  uo*I*(r2  - b2)/[(2*pi*r*(a2  - b2)] = uo*I*/(2*pi*a) at r = a.

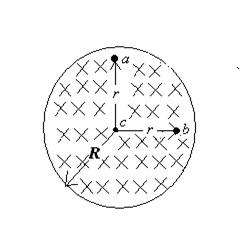
             d. B = 0 since the current enclosed is  ZERO.

 

3.  (30 points)  The figure shows a uniform magnetic field  confined to a cylindrical  volume of radius R.  As you can see the magnetic field vector points IN.  Consider a cross section  of the volume of radius R lying along the page and points  a, b, and c  lying in the circular area. The magnetic field magnitude is changing according to  the following formula:  

,  for t  0. This  problem uses symbols only. Answer in terms of given symbols and other possible constants. (Point a is a distance r above the center, point b is a distance r to the right of the center, and point c is at the center.)


 (a) (19 points) What are  the magnitude and direction of the electric field at point a for t  0.? Please indicate the direction by drawing an arrow with the tail at the point.

(b) (7 points) What are the magnitude and direction of the electric field at point b for t  0? Please indicate the direction by drawing an arrow with the tail at the point.

(c) ( 4 points) What must be the  electric field magnitude at point c for all t  0? Explain briefly.

 

SOLUTIONS:

        a. Points right. E = (r/2)*|dB/dt| = (r/2)*(Bo/tau)e –t/tau) =

        b. Points down. E = (r/2)*|dB/dt| = (r/2)*(Bo/tau)e –t/tau)

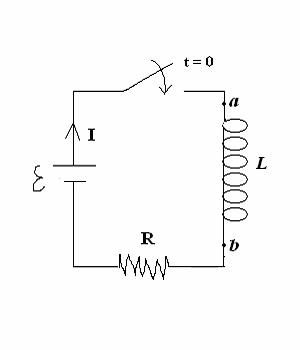
        c. E = 0, since r = 0 in  formula E = (r/2)*|dB/dt|

 

4.   (30 POINTS)   In the LR CIRCUIT  below, the current is zero at t  = 0 when the switch is closed.   The battery voltage is ε = 50.00 (V).  Assume R = 100.00 Ω. It takes 4.00 x10 -3 seconds for the current I to reach 0.250 (A). 

(a) (15 points)  How long after the switch is closed will  the current I reach 0.400 (A)?

(b) (5  points) At t = 4.00 x10 -3 seconds which point in the circuit has the higher voltage,  point a or point b?  Circle  one and explain. 

(c) (2 points)  What is the inductance L of the inductor?


(d) (8 points)  What is the difference  in voltage Va – Vb at
t = 4.00 x10 -3 seconds? 

 

SOLUTIONS: SEE TEST #3 , PROBLEM ON RC circuits. See QUIZ

10.            a.  I = ( 50.00/R)*(1 - e-t/T) (A)  . That is:
0.250 = 0.500*(1 - e-t/T) (A) or 
0.500 =  1 -  e-t/T
e-t/T  =  0.500
0.004 s = -(L/R)*ln(0.500). FIND L/R = T = 5.77x10 -3 (s). THEN SUBSTITUTE:
0.400 = 0.500*(1 - e-t/T) (A) or t =  =9.29x10 -3 (s) as you might expect.

                   b. TERMINAL a HIGHER,  to oppose increase in I.

                c.  L = -0.004 s*R/[ln(0.500)]   =  0.577 H

                d.  Vab = L*dI/dt = (50.00/L)* e-t/T = 25.00 (V) or
     Vab = battery voltage – voltage across resistor =
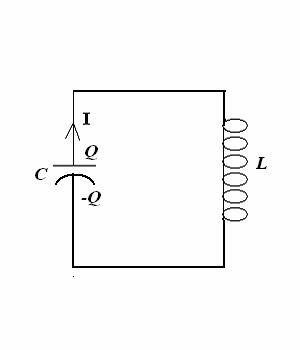
     50(V) –  0.250*100 (V) = 25.00 (V)

 

 

 

5. (20 points) LC CIRCUIT: A 20.00- µF capacitor is fully charged by a 100.00-V battery, then disconnected from the battery and connected in series with a 0.280-mH inductor at  t = 0.  Thus, the initial current I = 0.
See circuit below after the charged capacitor is connected to the inductor.

 

(a)  (2  points)   What is the angular oscillation frequency ω of the circuit?
(b)  (2 points)    What is the maximum charge Qmax on the positive capacitor plate?
(c)  (8  points)   What is the energy stored in the capacitor at t = 0?

(d)  (8 points)    Using conservation of energy, find  the magnitude of the current I when the charge Q on the capacitor reaches  one-half the maximum charge Qmax.  In other words, find I when Q = Qmax/2.

 

SOLUTIONS:

                 a. w2 = 1/LC = 13360 rad/s.

                 b. Qmax = C*[100.00 (V)] = 0.002 (C)

                 c. UE = (1/2)*Qmax2/2C = 0.10 (J)

                 d.   (1/2)*L*I2 + (1/2)*Qmax2/4C  + (1/2)*Qmax2/2C;
           I = 23.1 (A)  

 

 

6. (10 points) A transformer connected to a 110–(V) (rms) ac line is to supply 11.0 (V) (rms) to a portable electronic device. The load resistance R in the secondary is 5.00 Ω.

(a) (2 points) What should  the ratio of secondary  to primary turns of the transformer be? Note: “Secondary” refers  the portable device’s load and   “primary” refers to the ac-line.   

(b) (2 points) What rms current I2 must the secondary supply to the load? 

(c) (2 points) What average power is delivered to the load? 

(d) (2 points) Based on your answer to (c), what is the average power I1*V1 delivered by the ac-line?    Hint: Use conservation of energy.  

(e) (2 points) What is the current I1 drawn by the ac line?

 

SOLUTIONS:

                  a. 1/10

                   b. I2 = (11/5) (A) = 2.2 (A)

                  c. (11/5) 2*R = (11/5) 2*5 = (121/5) Watts = 24.4 (W)

                  d. I1*V1 = (121/5) Watts = 24.4 (W)

                          e.  I1 = (1/110)*(121/5) = (121/550) (A) = 0.220 (A).


7.  EXTRA CREDIT.  (12 POINTS) An  LRC series circuit is driven by a  voltage source εosinωt, where εo= 10.0 V. R = 150.0  ohms and L = 25.0 mH. Note:  1 mH = 10-3 H. The circuit’s  resonant frequency is ωo = 6.28 x 10 3 rad/s.


(a) (2) If the resistor value R is tripled, would the resonant frequency change? Yes or No . Circle one.  

(b) (4)  What is the capacitance C?

(c) (3) If the voltage source frequency ω = ωo , then what is the value of  the impedance Z?  

(d) (3) If the voltage source frequency ω = ωo , then what is the value of current amplitude Io?  
SOLUTIONS:

                    a. wo2 = 1/LC; THUS, NO.

                   b. C = 1/(L w2)  = 1.0x10 -6 F.

                   c. Z = R

               d.  Io  = Vo/R