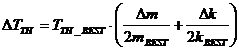SEE DOCUMENT END FOR SAMPLE DATA
In this experiment, you measure the parameters --mass m and spring constant k --- of an oscillating system and check whether the period T is as theory predicts. Consider the mechanical oscillator illustrated in figures 14-1 and 14-2 of the textbook (Young/Freedman) . At equilibrium, the mass has zero force on it; there the spring is neither stretched or compressed. When x is negative, the spring is compressed. Otherwise it is stretched. Fx = -kx is the x-component force causing the mass to return to the origin (x = 0) at all times; when the mass moves away from the origin, it slows down and when it moves toward the origin it speeds up. This explains all kinds of oscillators, whether they be molecules vibrating back and force in the warm pen you are using to write your lecture notes, air molecules oscillating back and force as my voice travels across the lecture room, or an “up and down” moving piece of string supporting a transverse standing wave such as on a guitar string. Such oscillations are everywhere, including your quartz watch. In Chapter 14, Newton’s second Law is applied to a mass m attached to a spring. According to Newton, the resultant force vector on an object of mass m at a given moment is m times the acceleration. In Chapter 14, we’ll explore this law in the many examples in which the force points towards x = 0. In this experiment you will test the theory for the special case of a vertically oscillating mass-spring system. The x component of force Fx = -kx leads, if block on stretched spring starts from rest, to: x= Acos(2πt/T) , where A is the amplitude and T is the period. See sections 14-2 and 14-3 especially figures 14-9, 14-10, 14-11, 14-12 and 14-14 and equation 14-13. On pages 443-4, we discover: T TH= 2π· (1) Note that you may choose the positive x direction to be downward which means x is positive when the vertical spring is stretched. To test the theory, you will measure the parameters (Mass m, Spring Constant k ) that appear in the theoretical expression for T to obtain a theoretical value TTh. ---see equation 1. By a timing procedure, you will directly measure an experimental value TEX, and then compare TTh with TEX . (See attached data sheet. ) In particular, you do the following for the mass-spring system: (a) Measure the parameters m and k that appear in your expression for the period in equation (1) and use them to compute TTH. (b) Measure the time t for a known number of cycles n (n = 10) and compute the experimental value of the period TEX = t/n. You will measure Tex 5 times and compute the average TEX_BEST. From this, you will also compute STDM or R/2 (R = max – min for the 5 trials. ) like you did in the lab on centripetal acceleration; this gives the statistical uncertainty in multiple measurements when the random errors are larger than the instrument error in a single, “simple” measurement. The instrument error is ΔT inst = 0.001 s /n or 0.0001 s/n ( where n = 10), depending on the timer resolution. CHECK TIMER RESOLUTION. The uncertainty ΔTEX you choose will either be ΔT inst or the statistical uncertainty (STDM or R/2) , whichever is larger. See attached data sheet. In either case, the uncertainty is rounded to just one digit and we round the average (“best”) value to the same decimal place. (c) Compute the uncertainties in the values TEX and TTH, then test the proposition that TTH = TEX using the criteria we used in centripetal acceleration lab: |TEX – TTH| < 2(ΔTEX + ΔTTH), PROCEDURE YOU will hang a tapered spring vertically from a support with the small end of the spring at the top. This spring taper direction is important for an accurate reading. The narrowing of the spring’s diameter toward the top allows the spring to stretch uniformly along its entire length. The narrowing toward the top means the upper half of the spring is stiffer than the lower half. This stiffness “gradient” is necessary because the upper part supports the weight of the lower part and so must be stiffer if it is to have the same stretch per unit length as the lower. (Q-1) You will add a mass of value m = 0.30 kg as suggested by data sheets, both sample and blank, and allow the system to oscillate up and down. Remember, the hanger already has mass 50 g, so you will add 0.250 kg. The formula for the period is given by equation (1) but there is one complication that has to do with the correct value of the mass. While the system vibrates up and down, different parts of the spring move at different speeds. The effective mass ms,Eff of the spring adds to the system’s inertia and kinetic energy storage capacity. It turns out that the mass m includes both 0.30 kg and one- third of the mass of the spring; a calculus derivation shows that ms,Eff = ms/3, where ms is the spring mass. You may enter this expression under (Q-1) of the attached data sheet. SH0W DERVIATION ON SEPRATE SHEETS. (Q-2) Beginning with equation (1), it is easy to derive (using Math 1 and 3 methods) the expression for the uncertainty in the theoretical value TTH of the period : (2) The expression contains the “best “ values from discussions below. Δm and Δk are the uncertainties in the oscillating mass m and spring constant k discussed below. (Q-3) To find the value of the spring constant k, use a sliding caliper jaw to record the position x’ of the bottom of the weight hanger with weights of mass M = 100, 200, 300 , 400 and 500 grams (g) suspended from the spring. Plot values of force in newtons vs x’ in meters and find the spring constant k in N/m with uncertainty Δk. Note: The uncertainties in x’ and the hanging masses M should be very small . Thus, the precision of your value of k will be limited by the graphing process. Thus, you can proceed without using error bars which will be discussed in a future lab. The least squares fit computational method for determining the slope will also be addressed later. The following suggestions are for graphically measuring, or estimating, the slope k: Compute ΔFs and Δx as a check using graph paper w/ data sheet.) THEN USE LOGGER PRO WITH A BLANK EXPERIMENT-MAKE NO USB CONNECTIONS TO PC, JUST OPEN PROGRAM W/O GREEN UNIT. PLOT YOUR POINTS IN THE TABLE ON THE LEFT WITH THE FORCE VALUES IN THE RIGHT COLUMN AND THE STRETCH LENGTHS IN THE LEFT. SLECT AND PRESS REGRESSION LINE BUTTON AND COMPUTE THE SLOPE AND THE RSME OF THE LINE; NOTE : RMSE = CHANGE IN k = Δk.
	(Q-1)
	Using calculus, Ms Eff = ms/3, where  is the spring mass.
	(Q-2)  Using calculus, it is easy to derive ,
	(Q-3)  M(kg)	Fs(N), using g = 9.8 m/s^2.	x' (m)
	0.100	0.98	51.95  (cm) = 0.5195 (m)
	0.200	1.96	61.70  (cm) = 0.6170 (m)
	0.300	2.94	71.65 (cm) = 0.7165 (m)
	0.400	3.92	81.40 (cm) = 0.8140 (m)
	0.500	4.90	91.35 (cm) = 0.9135 (m)

                                                    (Q-4)

masses related to total mass m
ms	171.90  = 0.17190 (kg)
msEFF	57.350  = 0.057350 (kg)
mo	300.00  = 0.30000 (kg)
mBEST	357.350  = 0.357350 (kg)

Note that the uncertainty in each measurement is considered to be 1 g.   Thus Δm_s = 1 g and Δm_o = 1 g. Since m = m_sEFF  + m_o,  Δm =  1g + 1 g/3 = 1.33333 g = 1 g if rounded to one sig. fig.

CORRECTIVE  NOTE: This last conclusion may be an overestimation and lead to conceptual inconsistencies since you used a mass scale which has a smaller uncertainty than 1 g.  In the centripetal force lab, we said the uncertainty in mass scale measurements is  (1/4)*(0.1 g) = 0.025 g = 0.03 if rounded. So a better approximation would be Δm = 0.025 + 0.025/3 = 0.03333 = 0.03 g if rounded down.  This dovetails with the 1/100th place precision of the mass.

(Q-5)
We are now in the position to  find the theoretical period given by formula (1): 
T = 

 2π· (1)

or T² = 4*pi²*(0.357 kg/10.0 N/m). 

This leads to T_{TH_BEST} = 1.18717 seconds, where the underlined 8 indicates there are only three sig. figs.  Now we have  a "benchmark" 
for the experimental value of T which I am about to compute; see below. 

Before we address the direct measurement of T , let's find the uncertainty in the theoretical value ΔT_TH    given by formula under (Q-2):

(1.18717)*( 1.3333/714.700     +     0.03125/20.0) = (1.18717)*( 0.000186554     +     0.0015625) = (1.18717)*( 0.00342804)  = 0.0040697  = 0.004  if rounded down to one sig. fig.  

If you  use the more accurate condition of 0.025 g for the uncertainty, we get:  

(1.18717)*( 0.0333/714.700     +     0.03125/20.0) = (1.18717)*( 0.00004663865546     +     0.0015625) = (1.18717)*( 0.001609138655) = 0.001910321138 = 0.002 if rounded down to one sig. fig.  

These errors seem inconsistent with the precision of the reported average  T_{TH_BEST} = 1.18717 seconds, which is precise only to the 1/100 th place.  It is impossible for the third decimal place (1/1000th place) in the uncertainty to be meaningful (as in  0.004 or 0.002)  when the average period T_{TH_BEST}  is precise to only the 1/100th place.  Thus,  one might conclude that the error is "zero."

n	time for n cycles  (s)	TEX = t/n   (s)
10	11.7061	1.17061
10	11.7823	1.17823
10	11.6224	1.16224
10	12.1926	1.21926
10	11.7945	1.17945
	TEX_BEST =	1.181958 = average
	R/N=	(1.21926-1.16224)/5 = 0.011404
	ΔT inst =	0.0001/10 = 0.00001
	ΔT =	0.011404 = 0.01 if rounded to one sig.fig.

Note that in this case, since the uncertainty is 0.01 s  rounded to the 1/100th place and the average period is precise to the 1/100,000th place, then 
you would report the answer by rounding down the average to the same place: T_EX = 1.18 (s) +/-0.01 (s). Note that this is very different from the previous  example where the precision of the average ("best") was less than that of the  uncertainty,  in which case the uncertainty is taken as "zero."  

(Q-6)

Now check the discrepancy. |T_EX – T_TH| < 2(ΔT_EX + ΔT_TH),

| 1.181958 - 1.18717 | < 2*| 0.011404 + 0| = 0.022808

Now, the left hand side is zero since 1.181958  - 1.18717 = - 0.005213 = 0. Thus we can conclude that the theoretical  period equals the measured experimental period.