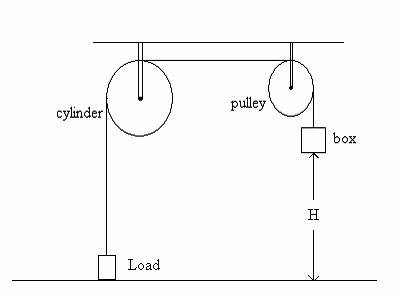
1. (40 POINTS) A cylinder and pulley have radii R_c = 0.150 m and R_p = 0.120 m, respectively. Consider these two rotating objects to be uniform solid cylinders (i.e. disks) with masses M_c = 5.00 kg and M_p = 2.00 kg, respectively. The cylinder and pulley turn without friction about their stationary axles that pass through their centers.

A light rope is wrapped around the cylinder. One side of the rope passes over the pulley and has a 4.00 kg uniform rectangular block suspended from its free right end. The other side has a 2.00 kg uniform rectangular -shaped load suspended from the rope’s left free end. The box and load have the same vertical thickness. The box is released from rest when its bottom surface is an initial height H = 6.00 m above the ground. The box descends and the load rises (ascends) as the rope turns with the cylinder and pulley. There is no slippage between rope and the cylinder and pulley surfaces.

(a) (30 points) Find the common speed v of the box and load when the box has fallen 3.00 m.

(b) (10 points) What is the ratio ω_p/ω_c of the pulley’s angular velocity to the cylinder’s angular velocity while the box is descending?

SOLUTION:
REFERENCE---see # 4 test 4.  

(a) Use conservation of energy.  Let m be the mass of the load and m' be the the box mass. Note: On the left hand side, h = 6.0 m and the right side: h' = 3.0 m

0     +  m'gh = (1/2)*m'*v² + (1/2)*m*v^{2  +} (1/2)*I_c*w_c²  +  (1/2)*I_p*w_p²  +  m'gh'  +  mgh',

where v = w_c*R_c    =  w_p*R_p  or  w_c = v/R_c   and  w_p =  v/R_p. Make those substitutions to get v = 3.52 m/s using

I = (1/2)*M*R² for each rotating object.  

(b) Since v = w_c*R_c    = w_p*R_p , we see the ratio is 1.25.

-------------------------------------------------------------------------------------------------------------------------------
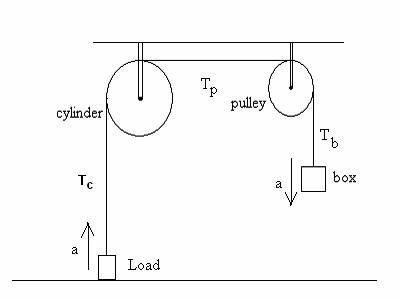
2. Extra Credit (15 POINTS. No penalty if not done.) Referring to the previous problem,

(a) (6 points) what is the magnitude a of the common acceleration of the box and load?
(b) (9 points) what are the tension magnitudes
(i) T_b in the section of string between the pulley and the box.
(ii) T_p in the section of the string between the pulley and cylinder
(iii)T_c in the section of the string between the cylinder and the
load?

SOLUTION USING CHAPTER 10 METHODS: REFERENCE---see # 4 test 4.  

(a) Let the tension in string section connected to box  be T_b , tension in  section between  pulleys be T_p ,

and tension in  section between  cylinder and load  T_c .

We have four  easily managed equations:

m'*a = m'g - T_p

m*a = T_c  - mg. 

I_p*(alpha_p) = R_p*(T_b  - T_p)

I_c*(alpha_c) = R_c*(T_p - T_c)

the latter  two of which  may be re-written as

I_p*a/R_p² = T_b  - T_p

I_c*a/R_c² = T_p  - T_c   .

NOTE: a = alpha_p* R_p  = alpha_c * R_c ,  which we used in the substitutions just above .

If you add these four equations, the tensions cancel and you can get a, the linear ( TANGENTIAL) acceleration of

the box and that of a point  on the rim of either pulley.

a = (m' - m)g/( m + m' + I_p/R_p² +  I_c/R_c² )   = 2.06 m/s².

Note if you use v² = 2*a*h, where h = 3.00 m you get v = 3.52 m/s. 

(b) To get  the tensions go back to the above equations and substitute to get:

T_b  = 30.9 (N),   T_p  = 28.9 (N)  and  T_c  = 23.7 (N)

 ---------------------------------------------------------------------------------------------------------------------------------------------------------

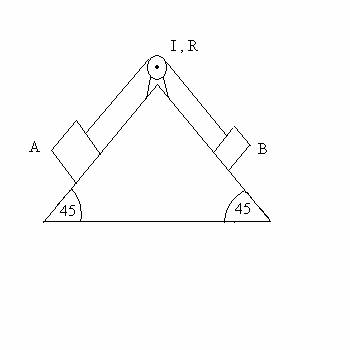
3. (40 POINTS) Two blocks are on a double incline whose surfaces make angles of 45 degrees with the horizontal. Block A on the left is connected to a rope that is wrapped around a pulley. The other end of the rope is connected to Block B on the right. The surfaces are frictionless. The pulley has I = 0.500 kg*m² with respect to the fixed horizontal axis of rotation through the center marked by the dot. The pulley radius is R = 0.200 m. See labels on the pulley below.
The block on the right has mass m_B= 5.00 kg, and the block on the left has mass m_A = 8.00 kg. Assume the system starts from rest.

(a) (2 points) In the figure below, what direction does the pulley rotate, clockwise or counter clockwise? Circle one.
(b) (16 points) Compute the magnitude |α | of the pulley’s angular acceleration about the axis shown.
(c) (10 points) Compute the tension magnitude T_B in the section of string between the pulley and Block B.
(d) (10 points) Compute the tension magnitude T_A in the section of string between the pulley and Block A.
(e) ( 2 points) Referring to parts (c) and (d), should T_B be larger or smaller than T_A ? Circle one and explain.

SOLUTION USING CHAPTER 10 METHODS: REFERENCE---this is a combo twist on #16, 64, quiz 12.   It is actually

 very close to #16 by default.

(a) Counter-clockwise since mass A is larger than mass B.

(b) We have 3 easily managed equations:

m_A*a = m_A*g*sin 45 - T_A

m_B*a = T_B  - m_B*g*sin 45 . 

I*(alpha_\) = R*(T_A  - T_B)

the latter of which  may be re-written as

I*a/R² = T_A  - T_B

NOTE: a = alpha* R ,  which we used in the substitutions just above .

If you add these three equations, the tensions cancel and you can get a, the linear ( TANGENTIAL) acceleration of

 the box and that of a point  on the rim of  pulley.

a = (m_A- m_B)*g*sin 45 /( m_A  +  m_B + I/R²)   = 0.816 m/s²;  thus alpha = 4.01 rad/s². 

(b) and (c) : To get  the tensions go back to the above equations and substitute to get,

T_A  = 48.9  (N),   T_B  = 38.7 (N) .

| Tension A |>  | Tension B |.

--------------------------------------------------------------------------------------------------------------------------------------------------------

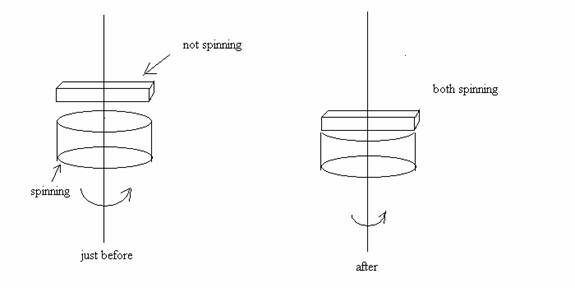
4. (13 POINTS) During the last week of class, a professor performs a classroom demonstration using a large wooden turntable in the shape of a flat uniform disk. The turntable has radius R = 1.00 m and a total mass of M = 4.00 kg. The turntable is initially rotating at angular velocity ω_i = 10.00 rad/s about a vertical axis through its center. Suddenly, the professor vertically drops a non-spinning uniform plank on the spinning turntable. You may model the plank as a uniform rod with length L equal to the diameter of the turntable. The plank mass is m = 2.00 kg. The plank lands on the turntable along the turntable’s diameter, sticks to the turntable’s surface and turns with the turntable without slipping. Below is a schematic of the system just before and after the plank lands on the turntable surface.


(a) (10 points) What is the common final angular velocity ω_f of the system after the plank lands on the turntable?
(b) (3 points) Assume the axis shown runs vertically up and down the page. What is the direction of the angular momentum of the system, up or down? Circle one and explain.

SOLUTION USING CHAPTER 10 METHODS: REFERENCE---this is a variation of #43, quiz 12. I also demonstrated this the last week of class with a hoop falling on a spinning cylinder ! 
(a)

L_iz = L_fz .
I_i*w_i = I_f*w_f. 
I_i = I_cylinder .   
I_f  = I_rod  +  I_cylinder  .  

Note: For a uniform rod, representing the plank,  I = mL²/12 where L is the rod length. Note: L = 2*R , where R is  disk radius and of course,  I_cylinder   = (1/2)*M*R².  If the rod is rigidly attached to the rotating solid cylinder about an axis through the center and perpendicular to the cylinder's face, then I_f =   mL²/12  +  (1/2)*M*R²  where L = 2*R.
  = 7.5 rad/s
(b) Up , from the right hand rule .

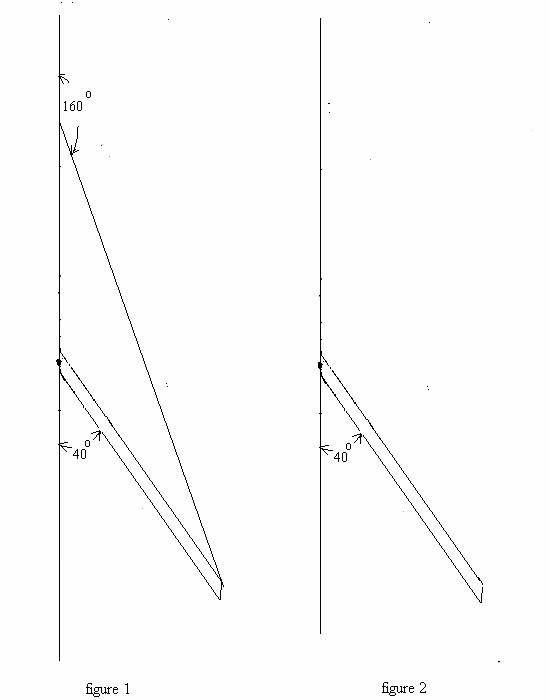
5. (40 POINTS) The uniform beam weighs 154.5 (N) ( i.e., mg = 154.5 N) and makes a 40 degree angle with a vertical wall. See diagram on next page. The beam is rigidly attached to the wall via a pivot. One end of a mass-less rope is attached to the beam’s right end and the other end to the vertical wall. The rope makes a 160 degree angle with the wall as shown in figure 1.
(a) (20 points) Compute the magnitude T of the tension force on the beam from the rope.
(b) (6 points) Compute F_h, the horizontal component of force of pivot on beam.

(c) (6 points) Compute F_v, the vertical component of force of pivot on beam.

(d)(8 points) Now suppose the rope is suddenly severed and the beam begins to swing clockwise about the axis at the pivot without the influence of the rope (i.e. T = 0). See figure 2. Thus, the beam makes an angle of 40 degrees with the vertical without the rope at this instant of time. For the following questions, you may model the beam as a uniform rod of length L = 1.00 m.
(i) At that instant, what is the magnitude of the torque on the beam
about the axis at the pivot?

(ii) At that instant, what is the magnitude | α | of the beam’s

angular acceleration about the axis at the pivot?
SOLUTION This is a variation of ALL BEAM PROBLEMS, quiz 13.
(a)   The angle between beam and rope is 20 degrees via simple geometry involving complimentary angles and the sum of the triangle's internal angles being 180 degrees. The torques are taken about the axis at beam's left end:
0 = (Lsin 20)*T  - (L/2)*sin 40 *mg, giving T = 145 (N) .
(b) Through your practice  with beam problems , it is easy to show the tension force makes an angle  of 70 degrees with the horizontal. Thus F_h = T*cos 70 = T*sin 20 = 50 (N).    
(c) Fv = mg - T*sin 70  = mg - T*cos 20 = 18 (N)
(d)  (i) torque = (L/2)*sin 40 *mg = 50 (N)

(ii) alpha = torque/I = 49.66/(mL²/3) = 9.45 rad/s².

----------------------------------------------------------------------------------------------------------------------------------- 

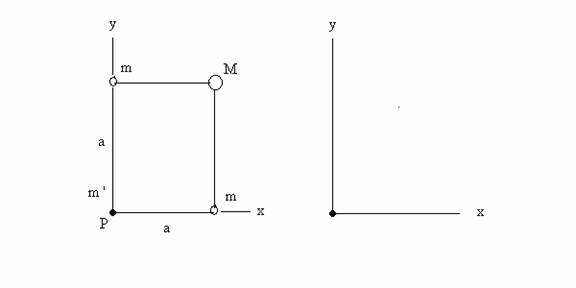
6. (25 points) Three uniform spheres are fixed at the three corners of a square of side a = 0.50 m. A 4^th sphere, of mass m ‘ represented by the dot, is placed at the lower left corner of the square—at point P. Note: The sphere in the upper right corner has mass M = 2.00 kg and the spheres in the upper left and lower right corners have equal masses m = 1.00 kg. The sphere in the lower left corner has mass m’ = 0.0150 kg.
See left diagram in the figure below.

(a) (5 points) What is the magnitude of the force on the sphere of mass m’ due to the sphere directly above it in the upper left corner.

(b) (7 points) What is the magnitude of the force on the sphere of mass m’ due to the sphere across the diagonal in the upper right corner?
(c) (1 point) What is the magnitude of the force on the sphere of mass m’ due to the sphere directly to the right of it in the lower right corner?
(d) (6) What is the magnitude of the resultant force on the sphere of mass m’ ?
(e) (6)What is the direction of the resultant force on the sphere of mass m’? Show this angle by drawing the resultant on the blank x-y axes in the correct quadrant. Label the angle the vector makes with the x-axis.
SOLUTION This is a variation of # 49 along with   #13,  52,   quiz 14.
(a) Gm'*m/a²  = 4.00 x10 ^-12 N .
(b) Gm'*M/(2a²) = 4.00 x10 ^-12 N .
(c) 4.00 x10 ^-12 N .
(d) X-component force =  4.00 x10 ^-12 N  + 4.00 x10 ^-12  cos 45  N . 
Y-component force =  4.00 x10 ^-12 N  + 4.00 x10 ^-12  sin 45  N . 
Using the Pythagorean Theorem: Magnitude = 9.66x10 ^-12 (N).

The force makes an angle of 45 degrees with the positive X-axis.

--------------------------------------------------------------------------------------------------------------------------------------------------

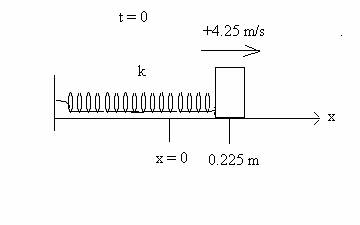
7. (15 points) A 2.00 kg frictionless block is attached to a horizontal spring as shown. The spring has force constant k = 300 N/m. At t = 0, the position x = 0.225 m, and the velocity is 4.25 m/s toward the right in the positive x direction. Position x as a function of t is:
x = A*cos(ωt +Φ ) , where A is the amplitude of motion and Φ is the phase constant.

(a) (8 points) Compute amplitude A
(b) (7 points) Compute phase constant Φ . For full credit indicate the correct quadrant.
SOLUTION: A VARIATION OF # 12, QUIZ 13 AND VIRTUAL LAB #2.
(a)  (1/2)*m*v² + (1/2)*k*x²   =(1/2)*k*A².
A = 0.414 m > 0.225 m.
(b) x(0) = A*cos Φ   = 0. 225  m  and -ωA*sin Φ   = 4.25 m/s  giving Φ  = -57 degrees (Quadrant 4) .