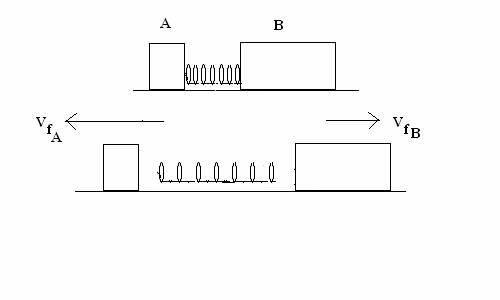
1. (40 points)  A block of mass m and a block of mass 3m are used to sandwich a mass-less spring with force constant k. In the diagram below m_A = m and m_B = 3m. The blocks are not connected to the spring and the spring drops to the surface after it has expanded. Initially the blocks are at rest on a frictionless surface and they are being held together so that the spring between them is compressed by an amount D from its equilibrium length. The blocks are then released, and the spring pushes them off in opposite directions. Shown below are the   final velocity components along the x-axis after the expansion. The following answers must each be expressed in terms of  symbols k, m and D.
(a) (20 points)  Find the final speed | V_fB | of block B.
(b) (20 points)  Find the final speed | V_fA | of block A.
SOLUTIONS:
(1/2)*k*D² = (1/2)*m* V_fA² + (1/2)*(3m)*V_fB 2   
m* V_fA + (3m)*V_fB    = 0.
Simultaneous substitution yields solutions for the speeds given by
  V_fA²   = (3/4)*(k/m)*D²  .

  V_fB2   = (1/12)*(k/m)*D²  . 

from which you take the positive square root of both sides to get final answers (speeds). 
COMMENT: This type of problem is universal in physics , whether you are exploring the Compton effect--the problems of  a free electron that absorbs a photon-- or, more directly,   the recoil  of a nucleus after it ejects a beta ray or some other decay product: BOtTOM LINE, you often need to use conservation of momentum and energy.

2. (40 points )  At t = 0, two masses  are shown at rest on a frictionless track that has two curved portions at either end and a central straight, horizontal section at the bottom.  The block of mass m is at the  top of the curved section and  slides down the track toward the right. It collides with a block of mass 2m  located  on the straight part of the track. The collision is elastic. The initial height H = 2.00 meters  and m = 1.00 kg.  



SOLUTIONS: 
(a)  mgH = (1/2)*mv² yields v = 6.261 m/s, the speed just before the collision.  Now use conservation of momentum:
mv +(2m)*0 = mv' + (2m)*v" and  v - 0 = v" - v'.
Solving these two equations simultaneously  we get v' = -2.087 m/s  and v" = +4.174 m/s. The last step is using conservation of energy to get  maximum heights--
 (1/2)*m*v'² = mgh'   and (1/2)*(2m)*v''²   = (2m)*g*h"
We get: (b) h' = 0.2222 (m) and (a) h" =  0.8888 (m) .      

 Clearly , from conservation of energy, when the two blocks are about to have  a second collision, block of mass of m has velocity + 2.087 m/s and the block of mass 2m has velocity -4.174 m/s.  
Recreate the same equation set as  above,  only with different numbers---
m*(2.087 m/s)  + (2m)*(-4.714 m/s) = mv_f' + (2m)*v_f" and  2.087 m/s  - (-4.174 ms) = v_f" - v_f'.
Solving  simultaneously  we get (c) v_f' = -6.261 m/s  and (d) v_f" = 0 ( stops) .
(e) (1/2)*m*v_f'² = mgh_f', giving h_f' = 2.00 (m) . 
COMMENT: If the system was allowed to act on its own under these ideal conditions, the same sequence of collisions, final speeds and heights would continue forever.  Motion would be periodic but not simple harmonic motion though. 
(a) (14 points) How high above the bottom will the block of mass 2m rise after the collision before momentarily  coming to rest?  

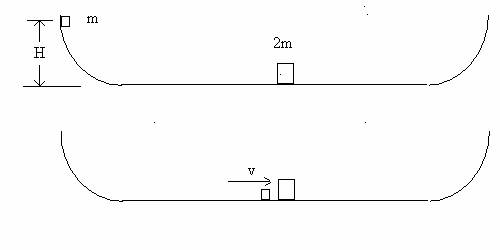
(b) (11 points) How high above the bottom of the track will the block of mass m rise after the collision before momentarily  coming to rest?  

            After rising to their maximum height, the blocks slide back down and collide a second time elastically on the horizontal track.  
(c) (6 points)  What is the velocity of the block of mass m immediately after the second collision? Give the magnitude and direction.

(d) (6 points)   What is the velocity of the block of mass 2m immediately after the second collision? Give the magnitude and direction.

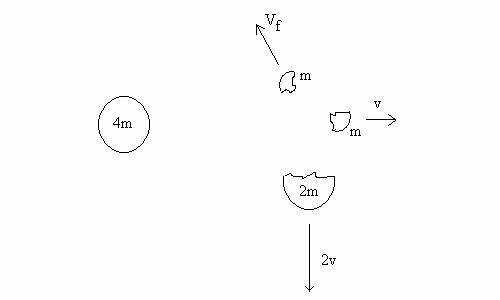
(e) (3 points) How high above the bottom will the block of mass m rise  after the second collision before momentarily  coming to rest?  

 

  

3.  (40 points)  You are on a Star Trek mission and observing an asteroid explode on your computer screen.  The asteroid of mass 4m is in deep space and  initially at rest. Then it bursts into three pieces. One chunk, of mass m, moves horizontally to the right with speed v. Another chunk , of mass 2m, moves in a direction downward at 90 degrees to the direction of the first piece. 

From this information, symbolically or numerically  find
(a) (20 points ) The magnitude V_f of the velocity of the final chunk.
(b) (20 points) The angle the final chunk’s velocity  makes with the horizontal.
SOLUTION:  
In general,   
sum of momentum in x direction  before collision = 
sum of momentum in x direction after collision 
AND
sum of momentum in y direction  before collision = 
sum of momentum in y direction after collision.

In this case, the sum of momentum before collision is ZERO IN ALL DIRECTIONS. 

THUS IN Y DIR:  0 = pos - neg (after) = m*V_f*sin theta  -  2m*2v
THUS IN X DIR:  0 = pos - neg (after) = m*v - m*V_f*cos theta.
OR 

m*V_f*sin theta   = 2m*2v
m*V_f*cos theta  = m*v
Divide the two equations to get
tan theta = 4. Thus, numerically  theta = 76 degrees and substituting theta  into either of the two equations symbolically yields V_f = 4.17v.  


 

 

 

 

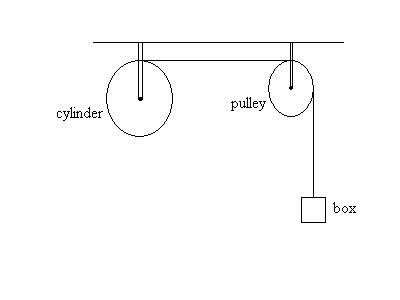
4 (40  points) The cylinder and pulley turn without friction about stationary horizontal axles that pass through their  centers. A light rope is wrapped around the cylinder, passes over the pulley, and has a 3.00 kg box suspended from its free end. There is no slippage between the rope and pulley or cylinder surface. The uniform cylinder has mass 5.00 kg and radius 40.0 cm.  The pulley is also a uniform cylinder with mass 2.00 kg  and radius 20.0 cm. The box is released from rest and descends as the rope unwraps from the cylinder .

  (a)  35 points)  Find the speed  v of the box when it has fallen a vertical distance h =  1.50 m.     

  (b) ( 5 points)  What is the ratio ω_p/ω_c  of the pulley’s angular velocity  to the cylinder’s angular velocity when the

box has fallen 1.50 m?

USE CONSERVATION OF ENERGY  AS SHOWN IN CHAPTER 9 . NOTE: YOU COULD SOLVE THE

PROBLEM USING  CHAPTER 10 METHODS BY FINDING THE TENSIONS AND LINEAR

ACCELERATION OF THE BOX;  ONCE YOU FIND THE ACCELERATION, WHICH IS CONSTANT,  YOU

COULD THEN FIND THE  SPEED  USING CHAPTER 2 METHODS.  Please send me an email at

nalexander@igc.org if you thought of that alternative method . I welcome your comments on this problem.  I am 

doing some research. - 

SOLUTION USING CHAPTER 9 METHODS: 

(a) KE_i + U_i  = KE_f + U_f

0     +  mgh = (1/2)*m*v² + (1/2)*I_c*w_c²  +  (1/2)*I_p*w_p² , where v = w_c*R_c    =  w_p*R_p  or  w_c = v/R_c   and  w_p =

 v/R_p. Make those substitutions to get v = 3.68 m/s using I = (1/2)*M*R² for each rotating object.  

(b) Since v = w_c*R_c    = w_p*R_p , we see the ratio is 2.

SOLUTION USING CHAPTER 10 METHODS: 

(a) Let the tension in string section connected to box  be T_p and  tension in  section between  pulleys be T_c. 

We have three easily managed equations:

m*a = mg - T_p    and 
  = 

I_p*(alpha_p) = R_p*(T_p  - T_c)

I_c*(alpha_c) = R_c*T_c

 

the latter  two of which  may be re-written as

I_p*a/R_p² = T_p  - T_c

I_c*a/R_c² = T_c   

NOTE: a = alpha_p* R_p  = alpha_c * R_c ,  which we used in the substitutions just above .

If you add these three equations, the tensions cancel and you can get a, the linear ( TANGENTIAL) acceleration of

 the box and that of a point  on the rim of either pulley.

a = mg/( m + I_p/R_p² +  I_c/R_c² )  .

To get  speed v go back to Chapter 2:

v² = 2*a*h and solve for v. 

(b) Since v = w_c*R_c    = w_p*R_p , we see the ratio is 2.