WORKSHEET DISCUSSIONS

WORKSHEET DISCUSSIONS (CHECK BACK FOR UPDATES)

UPDATE #1: NOTE THE CORRECTION TO #6, GRP2.

GRP1

1. SEE TEXTBOOK/CLASS NOTES. You should be able to derive this from memory

2. FIND THE INTERSECTION between a line that obeys y = -x and a concave down parabola with vertex at the origin Another way of looking at this problems is to assume an object is launched horizontally into open space. Find the time when the absolute value of x equals the absolute value of y: | x | = | y | for this parabolic path. Use x and y component projectile motion formulae in Chapter 3 for in the special case the initial launch angle is zero.

3.This problem #54, Ch. 3 is like the egg and the professor, #76, Ch. 2. Let us review #54 to compare. In 54, there was a non-vertical launch direction toward the front of the incoming boat. The horizontal displacement of the equipment from the launch point is x = Vo*cosa_o*t. Time t of course is obtained using Ch. 2 methods on the y- motion equations for projectile motion. Where V is the boat's speed, add V*t to the value of x to get the initial distance D of the boat from shore. D = (Vo*cos*60*)t + V*t, where t is found by solving -8.75 = (Vo*sin60)*t - (1/2)*g*t². In this problem you have to find the time from the y-motion as well:
(b) Solve for Vo in the diagram by realizing the two ships will have the same value of x when they met. In the x direction, it's like a 1 D"catch up" situation, like problem 2 on worksheet 1 dealing with "SIX MILLION DOLLAR MAN." That comment will help you deal with part (a) asking for a sketch of the x position of cannon ball and treasure ship. We have along x: D + (1/2)*a*t² = (Vo*cos45)*t, where t = 2*Vo*sin45/g = time of flight and D = 60 m ( 3 sig figs.) After eliminating the time t, plug the replacement into first equation and solve for Vo.

4. See section 3.4

5. Use equation 3.28 and the idea of a "instantaneous circle" configured to each point A, B and C on graph of an ellipse. Note the foci are given by the two open circles. Here is the configuration process to find the circle. At point A let an arc section of the circle coincide with the curved section in the vicinity of point A and you will form a small circle whose center is within the ellipse and to the left of the leftmost focal point . That circle will have a relatively small R. At point C let an arc section of the circle coincide with the curved section in the vicinity of point C and you will form a large circle whose center is OUTSIDE the interior region of ellipse. The circle will have a relatively large R. In all cases the instantaneous centripetal acceleration points to the center of the "instantaneous circle" you configured.

GRP2

1. This is a classic problem diagnosing whether or not you are behind in the class at this moment. This problems is almost like example 5.15; just replace the tension magnitude T by a force of magnitude F = 3.8 N at 30 degrees above the horizontal.
(a) See example 5.15
(b) sum of forces in y dir = 0 = pos - neg, where "pos" includes the normal force of magnitude N and the upward y component of the applied force and "neg" is mg, the weight magnitude.
(c) See example 5.15 and above notes.
(d) sum of forces in pos x dir = m*a = pos - neg = F*cos30 - f_k. where the friction force magnitude is a direct function of the normal force magnitude mentioned in part (c). Be careful.
(e) and (f) Use Ch. 2 methods

2. See Problem #28, Chapter 4, Quiz 5 or #33, CH. 6 or, more directly, Figure 5.64 for problem #67, Ch. 5. The poroblem is base d on a tru story. I saw a instructor do this at Chabot but only with a coffee cup on the car roof. I warned her/him before she took off and unwittingly became part of a grand physics experiment. Isolate each mass and refer to #Problem #28 at least for the set up.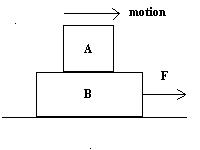

Your main concern is box A on top and not the surface between box B and the floor which could be assumed to be frictionless. But there must be friction between B and A if box A has any chance not not slipping with respect to the bottom box B as both accelerate together in the forward direction, positive to the right. If there was not friction between A and B, as you pulled on B, A would remain with the same value of x and drop down vertically to the floor in the y direction when B was completely pulled from under A.
ISOLATE A:
sum of forces in the x dir = m*a - = pos - neg = f_s - 0, where f_s is the static friction force magnitude. Set f_s equal to the maximum allowed and find acceleration x-component a. REVIEW SECTION 5.3

3.
(a) See example 5.16. Here and in that case the acceleration down the incline is zero. But in this case use static friction laws to get the angle using given coefficient.
(b) When it starts sliding down the incline the friction converts from static to kinetic, causing a drop in friction magnitude as seen in figure 5.19. In that case, will the acceleration magnitude be greater than zero? Explain and answer the requested questions.

4. See example 5.11, which helps us understand the idea of the contact force which is nothing more than F₁₂ = F₂₁ = F_C from NEWTON'S THIRD LAW.

ISOLATE: EACH MASS.

MASS 1:

sum of forces in x dir = pos - neg = m₁*a =F - F₁₂ - f_k1.

MASS 2:

sum of forces in x dir = m₂*a = pos - neg = F₂₁ - f_k2.

Set F₁₂ = F₂₁ = F_C AND SOLVE FOR ACCELERATION a AND CONTACT FORCE MAGNITUDE F_C. To find

f_k1 and f_k2 , use the kinetic friction laws after getting the normal force magnitude N for each block.

5. See problem #65, quiz 6. But now we have acceleration down the incline for mass M. For mass M, DOWN the plane is the pos x direction and let PERPENDICULAR and away from the plane surface be the pos y direction. For mass m assume vertically up on the page is the positive y direction. So write:
M*a = pos - neg = Mg*sin theta - T - f_k.
m*a = pos - neg = m*a = T - mg.
Solve these two equations for acceleration magnitude a and tension T symbolically. Abide by kinetic friction laws.

6. Let rightward be positive x and upward be positive y. Easy problem is you use Newton's first law in the x and y direction which says no acceleration occurs in said direction when the net force component is zero. Since you are looking for a range involving static friction this problem is like #7 next and group 3's #5 .
(a) Assume the block is about to slide down, which means the friction force is upward.
sum of forces in x dir = 0 = pos - neg = N - F*sin theta
sum of forces in y dir = 0 = pos - neg = F*cos theta + f_smax - mg.
Note f_smax = u*N, where u (pronounced "mew") represents the coefficient of static friction.
Make that substitution and solve the two equation for unknowns N and F symbolically.
(b) Assume the block is about to slide upward, which means the friction force is downward.
sum of forces in x dir = 0 = pos - neg = N - F*sin theta
sum of forces in y dir = 0 = pos - neg = F*cos theta - f_smax - mg,
f_smax = u*N, where u represents the coefficient of static friction.
Make that substitution and solve the two equation for unknowns N and F symbolically.
(c) Focus in PART (b) for this part.

7. THIS IS THE GRANDMOTHER OF ALL PROBLEMS, INTEGRATING ALL OUR CONCEPTS AT THE HIGHEST LEVEL: (i) ISOLATION, (ii) FORCE DIAGRAMS, (iii) RESOLVING FORCES INTO COMPONENTS ALONG X AND Y DIRECTION, (iv) sum of the forces in given dir = pos - neg.
Let rightward be positive x and upward be positive y. Thus x is along the horizontal not the incline since the motion and acceleration is horizontal. We use this convention in the banked curve situation of example 5.23. Assume the block of mass m is about to slide up the plane, which means the static friction force is down the plane.
ISOLATE MASS m:
sum of forces in x direction = m*a = pos - neg = N*sin theta + f_smax*cos theta
sum of forces in y direction = 0 = pos - neg = N*cos theta - mg - f_smax*sin theta. Thus,
m*a = N*sin theta + f_smax*cos theta
0 = N*cos theta - mg - f_smax*sin theta .

NOTE HOW WE USED CONCEPT (iii) on the inclined friction force, resolving components along the horizontal x and vertical y axes.

Note: f_smax = u*N; make that substitution into the above equations please.
Finally, if you look at the mass M and the mass m as a combined system you can write:
sum of forces in x dir = (m + M)*a = F - 0 = F. Thus, a = F/(m + M). Make that substitution into the first of the top two equations and solve for F in terms of symbols to get the result requested on your worksheet. Hint: When you divide the two equations , N will cancel out.

GRP3

Questions 1 to 3: See discussion questions for quiz 6 and 7 ---- # 16, 19, 20, 23 AND 24 --- dealing with circular motion.

1. RULE--The positive R direction is toward the center of the circle.
(a) m is the car mass.
Point A: sum of forces in R dir = m*V²/R = pos - neg = mg - N.
Point B: sum of forces in R dir = m*V²/R = pos - neg = mg - N, but guess what ? R = infinity at A !
Point C: sum of forces in R dir = m*V²/R = pos - neg = N - mg.
(b) Use the above equations but for m substitute m_d, the driver's mass. The normal force magnitude N now refers to the force of the seat on driver's bottom. See example 5.24. This is just like a Ferris Wheel ride !
(c) Use sum of forces in R dir = m*V²/R = pos - neg = mg - N and set N = 0.

2. sum of forces in R dir = m*V²/R = pos - neg = f_s - 0 = f_s, where f_s is the static force magnitude. Find the speed when that force reaches a maximum using static friction laws. This is like motion on an unbanked circular track (i.e. "side shows" in which young folks' cars spin out)

3. See example 5.21 , except now you have two inclined strings wires keeping the ball in a horizontal circle. Make appropriate adjustments as you "reverse" engineer the example . The components of the tension forces in the horizontal R direction must sum to the resultant CENTRIPETAL force mV²/R = pos - neg = pos ( there is no "neg" in this case):

sum of forces in y dir = pos - neg = T1*sin theta - T2*sin theta - mg, where T1 is given.

sum of forces in R direction = mV²/R = pos - neg = T1*cos theta + T2*cos theta.

NOTE: R, THE HORIZONTAL CIRCLE RADIUS, AND THETA, THE STRING INCLINE ANGLE, CAN BE FOUND USING THE DIAGRAM'S GEOMETRY.

4. See example 5.23.

5. More on this later, but it is like #6 and # 7, group 2.

6. More on this later, but it is like an elevator problem . Let the N be the magnitude of normal force of the scale on your feet. The normal force points away from the center of the circle of rotation. At the equator you are moving in a circle as you rotate with the Earth about its central axis running through the North-South poles.

Sum of forces in R dir = m*V²/R = pos - neg = mg - N. Solve for N using the given R, m and speed V, found from the time of one Earth rotation (24 hours converted to seconds) and the Earth's circumference.