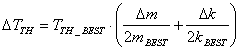In this experiment, you measure the parameters --mass m and spring constant k --- of an oscillating system and check whether the period T is as theory predicts. Consider the mechanical oscillator illustrated in figures 13-2 and 13-13 of the textbook (Young and Freedman) . At equilibrium, the mass has zero force on it; there the spring is neither stretched or compressed. When x is negative, the spring is compressed. Otherwise it is stretched. F_x = -kx is the x-component force causing the mass to return to the origin (x = 0) at all times; when the mass moves away from the origin, it slows down and when it moves toward the origin it speeds up.

This explains all kinds of oscillators, whether they be molecules vibrating back and force in the warm pen you are using to write your lecture notes, air molecules oscillating back and force as my voice travels across the lecture room, or an “up and down” moving piece of string supporting a transverse standing wave such as on a guitar string. Such oscillations are everywhere, including your quartz watch.

In Chapter 13, Newton’s second Law is applied to a mass m attached to a spring. According to Newton, the resultant force vector on an object of mass m at a given moment is m times the acceleration. In Chapter 13 and throughout the sequence, we explore this law in many examples in which the force points towards x = 0. In this experiment you will test the theory for the special case of a vertically oscillating mass-spring system. The x component of force F_x = -kx leads to the result that

x= Acos(2πt/T) ,

where A is the amplitude and T is the period. See section 13-2, especially figure 13.9 and equation 13-13. On page 425 we discover :

T _TH= 2π· (1)

Note that you may choose the positive x direction to be downward which means x is positive when the vertical spring is stretched. To test the theory, you will measure the parameters (Mass m, Spring Constant k ) that appear in the theoretical expression for T to obtain a theoretical value T_Th. ---see equation 1. By a timing procedure, you will directly measure an experimental value T_EX, and then compare T_Th with T_EX . (See attached data sheet. ) In particular, you do the following for the mass-spring system:

(a) Measure the parameters m and k that appear in your expression for the period in equation (1) and use them to compute T_TH.

(b) Measure the time t for a known number of cycles n (n = 10) and compute the experimental value of the period T_EX = t/n. You will measure Tex 5 times and compute the average T_{EX_BEST}. From this, you will also compute R/N (N= 5) or standard deviation of the mean S_m like you did in the Galileo lab this gives the statistical uncertainty in multiple measurements when the random errors are larger than the instrument error in a single, “simple” measurement. The instrument error is ΔT _inst = 0.001 s /n or 0.0001 s/n ( where n = 10), depending on the timer resolution. The uncertainty ΔT_EX you choose will either be ΔT _inst or R/N (or S_m) , which ever is larger. See attached data sheet. In either case, the uncertainty is rounded to just one digit and we round the average (“best”) value to the same decimal place.

(c) Compute the uncertainties in the values T_EX and T_TH, then test the proposition that T_TH = T_EX using the criteria we used in centripetal acceleration lab:

|T_EX – T_TH| < 2(ΔT_EX + ΔT_TH),

PROCEDURE

As in figure 13-17, you will hang a tapered spring vertically from a support with the small end of the spring at the top. This spring taper direction is important for an accurate reading. The narrowing of the spring’s diameter toward the top allows the spring to stretch uniformly along its entire length. The narrowing toward the top means the upper half of the spring is stiffer than the lower half. This stiffness “gradient” is necessary because the upper part supports the weight of the lower part and so must be stiffer if it is to have the same stretch per unit length as the lower.

(Q-1) You will add a mass of value m = 0.30 kg as suggested in figure 11-3 and allow the system to oscillate up and down. Remember, the hanger already has mass 50 g, so you will add 0.250 kg. The formula for the period is given by equation (1) but there is one complication that has to do with the correct value of the mass. While the system vibrates up and down, different parts of the spring move at different speeds. The effective mass m_s,Eff of the spring adds to the system’s inertia and kinetic energy storage capacity. It turns out that the mass m includes both 0.30 kg and one- third of the mass of the spring; a calculus derivation shows that m_s,Eff = m_s/3, where m_s is the spring mass. You may enter this expression under (Q-1) of the attached data sheet.

(Q-2) Beginning with equation (1), it is easy to derive (using Math 1 and 3 methods)
the expression for the uncertainty in the theoretical value T_TH of the period :


The expression contains the “best “ values from discussions below. Δm and Δk are the uncertainties in the oscillating mass m and spring constant k discussed below.

(Q-3)  To find the value of the spring constant k, use a sliding caliper jaw to record the position x’ of the bottom of the weight hanger with weights of mass M = 100, 200, 300 , 400 and 500 grams (g) suspended from the spring. Plot values of force in newtons vs x’ in meters and find the spring constant k in N/m with uncertainty Δk.
Note: The uncertainties in x’ and the hanging masses M should be very small . Thus, the precision of your value of k will nearly be limited by the graphing process. Thus, you can proceed without using error bars which will be discussed in a future lab. The least squares fit computational method for determining the slope will also be addressed later. To get k, we will use LOGGER PRO’S REGRESSION CURVE FIT and the RSME, an error in the slope.

(Q-4) Weigh the spring to find m_s and compute the effective mass m_s,Eff. Enter the value m_o = 0.30 kg.

Compute the total mass m = m_s,Eff + m_o. Use this value along with k_best to find T _TH = 2π·
_{Compute the uncertainty ΔTTH assuming an uncertainty of 1 g for you mass measurements or use values given in class discussion using least counts. . See (Q-2) and (Q-3).}

_{(Q-5) Suspend 0.30 kg from the spring, displace it slightly and determine the experimental period TEX.}

_{Make at least 5 trials and count at least 10 cycles for each trial:}
You will measure T_EX 5 times and compute the average T_EX-BEST. From this, you will also compute R/N, where N = 5; this gives the statistical uncertainty of multiple measurements when the random errors are larger than the instrument error in a single, “simple” measurement. The instrument error is ΔT _inst = 0.001 s /n or 0.0001 s/n ( where n = 10), depending on the timer resolution. The uncertainty ΔT_EX you choose will either be ΔT _inst or R/N (or S_m) , which ever is larger. In either case, the uncertainty is rounded to just one digit and we round the average (“best”) value to the same decimal place.

(Q-6) Compare the discrepancy between the theoretical and experimental values to the sum of their uncertainties.