. ( 50 POINTS) Below is a model for a pulsed laser used in science  and medicine. The interior of the pulse  can  represented by an  EM plane wave with frequency f = 2.50 x10 ¹⁴  Hz. The magnetic field 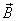  oscillates vertically  back and forth along a line that makes a 45 degree angle with the x and y axes. The magnitude of the magnetic field is 8.00x10 ^-9 T .  At a given instant the magnetic field makes an  angle of 45 degrees with the negative x–axis. The  arrow is labeled by the magnitude B of the magnetic field .  As shown by the dot centered within the little circle,

the  wave’s propagation direction is OUT of  the page.

 

(a) (17 points)  What is the direction of the electric field vector. Draw an arrow clearly on the x-y axes below. Draw the tail of the arrow at the origin.  What angle does the electric field make with the horizontal? Indicate and label  this angle in your diagram.
(b) (18 points) )   If 9020 wavelengths are found within the pulse, the how long ( in seconds) did the pulse last?    

(c) (15 points) Suppose the pulse is transmitted from a laboratory on the surface of the Earth toward the Moon. If the reflected pulse (i.e., reflected off the Moon’s surface) is received at the lab 1.30 seconds later, then what is the distance between the laboratory and the Moon’s surface?  (Assume the pulse is not affected by the Earth’s atmosphere; the Moon has no atmosphere.) 

 SOLUTIONS:
(a) The electric field vector points in the second quadrant and makes a 45 degree angle with the negative x- axis.
(b) c*t/wavelength = 9020, where wavelength = c/f. Thus, after substituting we get:
f*t = 9020 and t =  36x10 ^-12 seconds or 36 picoseconds. 
(c) ct/2 = distance= (1/2)*(3x10 ⁸ m/s)*(1.30 s) = 1.95x10 8 m.

 -----------------------------------------------------------------------------------------------------------------------

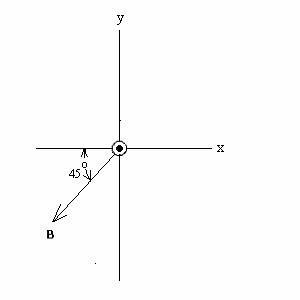
2. (50 POINTS)  The  upright object shown below is to the left of a  concave  mirror   with a focal length of 0.25 m (not shown). The object produces a real image  which is one third the size of the object.    

 

(a) (30 points)   How far from the mirror is the object?
(b) (3  points)  Is the image upright or inverted (upside down)?   Explain.
(c) (13 points) How far from the mirror is the image?

(d) (4  points)  On the diagram above sketch the mirror on the right of the object.  Draw the image by ray tracing as we did in class. Ray trace by drawing two rays from the tip of the arrow shown, one parallel to the axis and the other  intersecting the  point where the  mirror  crosses the axis.  Label the object distance d_o and image distance d_i. 
SOLUTIONS: 
(a) m = -1/3 = - di/do, so that do = 3*di . Thus 1/f = 1/di   + 1/do = 4/do and do = 4*f = 1.0 m.
(b) inverted since m < o.
(c) di = do/3 = 0.333 m
(d)  See class notes or check out figure 23.14 and COMPARE  with figure 23.16.

 

 -------------------------------------------------------------------------------------------------------------------

 


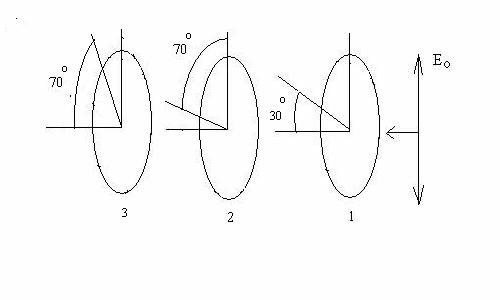
3.  (50 POINTS)  A beam of vertically polarized light with intensity 41 W/m² is sent leftward through three polarizing sheets. The vertically polarized wave is shown below moving   toward Sheet 1.  The polarizing direction of  Sheet 1 makes an angle of 30⁰ with the horizontal.  The polarizing direction of  Sheet 2 makes an angle of  70⁰ with the
vertical. The polarizing direction of  Sheet 3 makes an angle of 70⁰ with the horizontal.  




(a)  (17 points) What is the Intensity of the light after it passes through Sheet 1 before reaching  Sheet 2.   
(b)  (17 points)  What is the Intensity of  the light after it passes through   Sheet 2 before reaching Sheet 3?

(c)  (16 points)  What is the Intensity of  the light after it passes through   Sheet 3?

 SOLUTIONS:  
(a) 41*cos² 30 = 10.3 W/m²  .
(b) 10.3*cos² 10 = 9.99 W/m²  .

(c)  9.99*cos²  50 = 4.13 W/m²  .

 ----------------------------------------------------------------------------------------------------------------------

 

 

 

 

4.  (50  points) In a university lab experiment, a plate of glass is placed above  a container of water with the same lateral dimensions. The plate is parallel to the water surface. The glass plate and water are separated by an air gap of thickness t.  Light of wavelength 615 nm falls  perpendicular  to the plate and water.   

 

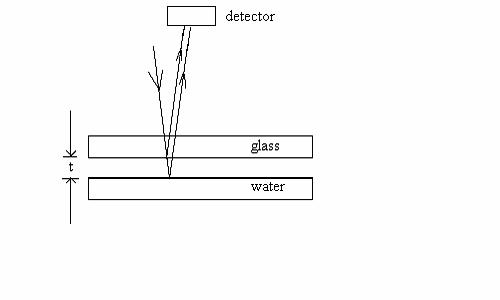
(a) (17 points)  What  minimum thickness t will produce  constructive  interference at the detector?

(b) (17 points)  Suppose the air gap between the plate and water  has the minimum thickness t you computed in part (a). Suppose  you raise the glass above the water surface and increase the air gap thickness until the signal at the detector first becomes  ZERO.  What is the new thickness t’ ?

 (c) (16 points)  Suppose the air gap between the plate and water  has the thickness t’  you computed in part (b). Suppose  you further raise the glass above the water surface and increase the air gap thickness.  What is the next thickness t”  that will produce constructive interference?
 
SOLUTIONS:
(a) 2t = wavelength /2 so t  =154 nm
(b) 2t = wavelength  so t = 308 nm
(c) 2t = (3/2)*wavelength so t = 461 nm.   
---------------------------------------------------------------------------------------------------------------------------

 

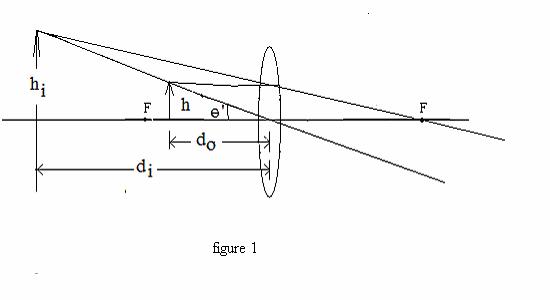
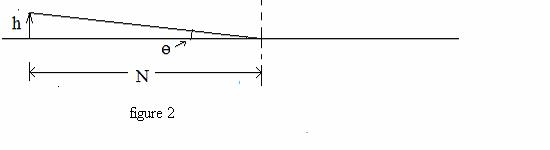
5. ( 51 POINTS) A magnifying glass has focal length f =  8.5 cm.  The magnifying glass is  used to read print (the object) placed a  distance  d_o =  7.5 cm from the lens.  See figures 1 and 2. Note that N = near point distance = 25 cm.
(a) (3 points)  Is the image of the news print virtual  or real ? Explain.

(b) (20 points) What is the image position  d_i  ?
(c) (8 Points) Using the definition of M, compute the angular  magnification M = θ’/θ. See figures 1 and 2.  
(d) (10 points) What would be the  angular magnification M if this lens forms a virtual  image at the person’s near point, assumed to be 25 cm away from the lens?
(e) (10 points) What would be  the angular magnification M  if the eye is fully relaxed and the lens forms  a virtual image essentially at d_i = - ?
SOLUTIONS:

(a)virtual image from the diagram
(b) 1/8.5 = 1/7.5   + 1/di so  di = -64 cm
(c) M = (h/do)/(h/N) = N/do = 3.3 x
(d) N/ f    +  1 = 3.9 x
(e) N/f = 2.9 x

 

 

 ----------------------------------------------------------------------------------------------------------------

 

  

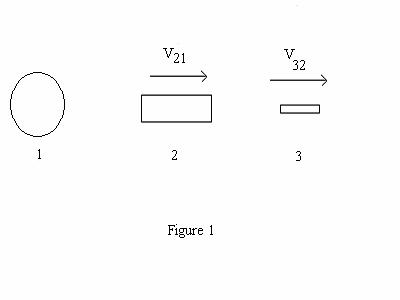
6. ( 20 points) A United Nations observer on Planet  Earth (1) remotely views  two vehicles in space.  A small rocket (3) has been  fired from a large rocket (2).  Rocket 3’s  velocity  relative to rocket 2  is V₃₂ = 0.600c. Rocket 2’s velocity relative to the Earth is V₂₁ = 0.600c.  See Figure 1.

(a) (13 points) Find the  velocity V₃₁  of  rocket 3 relative to the Earth.

(b) (2 points)   Explain why the answer to part (a) should  be less than the speed of light c.

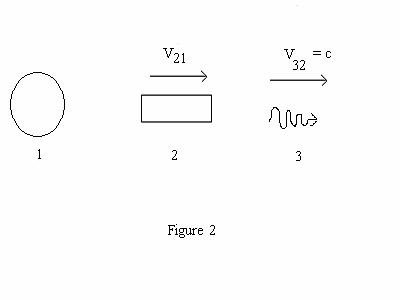
(c) (5 points)  See Figure 2 on the next page. Suppose  rocket 2 sends out a pulse of light (3) . In this case  V₃₂  =c.  Assume Rocket 2’s velocity relative to the Earth is V₂₁ = 0.600c . Using the method and formulas you used in part (a) , compute the  velocity V₃₁  of  the light pulse  relative to the Earth. Does your answer

make sense? Explain.
SOLUTIONS:
(a) V₃₁ = (V₃₂ + V₂₁)/(1 +  V₃₂*V₂₁/c²)  = 1.2*c/1.36   = 0.882  *c
(b) Objects with mass cannot exceed c since the relativistic  momentum discussed in Ch. 26 would become imaginary.
(c)  V₃₁ = (V₃₂ + V₂₁)/(1 +  V₃₂*V₂₁/c²)  = 1.6*c/1.6   = c.  The speed of light is the same in all reference frames !!
 

--------------------------------------------------------------------------------------------------------------------------

 

7. (12 points)    When a  beam  of UV (ultra violet)  radiation,  wavelength  285 nm,  falls on a metal surface,   the maximum  kinetic energy of emitted electrons is KE = 5.20x10 ^{– 19} J.  Note: h = 6.626x10 ^-34 J· s.

 What is the maximum kinetic energy KE’ ( in Joules) , when a beam of visible light,  wavelength 632. 8 nm,   falls on the same metal surface?

SOLUTION
h*f = = h*c/wavelength = 5.20X10 ^-19 J + W_o , where wavelength = 285 x10^{– 9} m.
W_o  = 1.77x10 ^-19. 

Now let    h*f' = h*c/wavelength' = KE'  + W_o    = KE'  +  1.77x10 ^-19  , where wavelength now is 632.8 nm = 632.8 x10^{– 9} m. Thus: KE' = 1.37x10 ^-19  J.