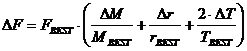In this experiment, you test whether  Newton’s  Second Law applied to uniform circular motion is correct.  In particular you will confirm the validity of the equation for the net force magnitude   F = Mv²/r. The general mathematical   background, subject to further class discussion, is here:
http://dept.physics.upenn.edu/~uglabs/lab_manual/Lab_Manual.pdf ;   See also
http://www2.truman.edu/~edis/courses/100/lab3.pdf for a more specific discussion subject to changes in this experiment. 

According to Sir Isaac  Newton, the resultant force vector on an object of mass M at a given moment  is M times the acceleration.  In Chapter 4, we explored this law with many examples in which the acceleration and force were constant. In this experiment you will test the theory for the special case of uniform circular motion. As discussed in  Chapters  5 and 8,  the acceleration , force and velocity magnitudes are constant ; only the direction of the  acceleration  and  velocity changes, that’s it.

The force causing this special motion is called the centripetal force , or “center seeking” force. It points to the circle’s  center  and has  constant magnitude F = mv²/r, where v is the speed ( i.e. velocity magnitude) and r is the  radius. It is not a new force, it  is only a name  we assign to any force that causes uniform  circular  motion, whether it be the gravitational and electrical  force  underlying   the Earth’s orbit  around the Sun  and  the electron’s motion around the nucleus,  respectively.    In the example of a rock  twirled in a vertical circle, the centripetal  force at any point is a combination of gravitational and tension forces.  See chapter  5.

To test the theory, you will measure the centripetal force magnitude F by two methods , static and dynamic:

(A)   A certain force F acting on the mass M is measured under static conditions by a weight mg.  We could call this the static value of F.

(B)   When the mass under goes uniform circular  motion this force should be equal to the centripetal force, and thus equal to Mv²/r   .  Thus we are testing whether the static and dynamic values are equal :

mg   =  Mv²/r   .  (1)

The experiment can easily be illustrated with a free body diagram provided by the instructor-- See figure 1, page 3,  of the experimental set up described here:

http://www2.truman.edu/~edis/courses/100/lab3.pdf

Let’s examine the  dynamic measurement (B). As the bob of mass M moves in a horizontal circle of radius r, the spring stretches and the vertically hanging string sweeps out a cylindrical surface whose sides are parallel to the central axis of rotation.  The spring force magnitude F_s , exerted on the bob when the spring stretches,   is automatically included in the both dynamic (B) and static measurements (A) of F.
 
In the dynamic case, the  total centripetal force has magnitude F = F_s , or  F_s   =  Mv²/r   .  In this derivation we assume that the spring connecting the bob to the central rod  is horizontal--as in the static case (A) . 

(A) STATIC MEASUREMENT. Make sure the axle-to-bob spring and the bob-to-pulley string are  precisely horizontal by measuring the height above the table at both ends, and then raising and lowering the pulley until the heights are equal.  You can make the platform parallel with the table by adjusting the clamps and knobs.

(Q-1) Make the static measurement of F taking 5 readings.  (See the Picket Fence Free Fall lab handout as a reference. ) Here is why we make multiple  readings. It’s  true that one way to state the precision of our readings   is to assume an   uncertainty     Δm _inst= 1 g for each “simple” measurement;  we  assume  the “instrument” uncertainty  is determined only by the measurement technique  . This means for m, written on grams (g),  the least significant digit is in the one’s  place with a 1 g  uncertainty.   This  uncertainty results from just measuring the mass needed to bring the bob pointer in alignment with the platform pointer. 

But the measurement  may be “non-simple”---it may have a larger uncertainty  than the technique uncertainty. There may be other random  errors besides those from just reading the mass after aligning the pointer. To cover this possibility,   we thus make the static measurement of F taking 5 readings. In this case, we  state the precision by taking  the difference between the minimum and maximum values  and dividing by N (where N = 5).   We call this quantity R/N.  Compute R/N .  Compare this approach with the Picket Fence Free Fall lab.   Compute the average (m_BEST) of the 5 measured masses m.  The uncertainty  you choose will either be   Δm _inst or R/N , which ever is larger.  In either case, the uncertainty is rounded to just one digit and we round the average (“best”) value to the same decimal place. As in the picket fence lab, the result is reported as
m_BEST ± uncertainty .

Also measure r, the distance between the axis of rotation to the center of the bob.   Take 5 readings.  Again, we can state the precision of our readings by assuming  only an “instrument” uncertainty  due to   random errors from just reading the instrument.  We will assume that the accuracy of any single reading with a meter stick is plus or minus ¼ of the smallest scale division of  0.1 cm. See page 36 here: http://dept.physics.upenn.edu/~uglabs/lab_manual/Lab_Manual.pdf

Thus , Δr_inst =  0.1/4 = 0. 025 = 0.03 for a single reading with  a meter stick . But the length r is measured from a difference of labeled marks on the stick.  It can be shown that a more accurate “instrument” uncertainty is  times the uncertainty for a single reading. See pages 49-50 here: http://dept.physics.upenn.edu/~uglabs/lab_manual/Lab_Manual.pdf

Δr_inst =  ·(0.1/4) = 0. 03525 = 0.04.   (2)

 But just  in case the  measurements are “non-simple”-- make the r measurement  taking 5 readings. Take  the difference between the minimum and maximum values  and divide by N (where N = 5) . This result is called   R/N.     Compute the average (r_BEST) of the 5 measured radii.  The uncertainty  you choose will either be   Δr _inst or R/N , which ever is larger.  In either case, the uncertainty is rounded to just one digit and we round the average (“best”) value to the same decimal place. As in the picket fence lab, the result is reported as r_BEST ± uncertainty .

(B)   DYNAMIC MEASUREMENT . To measure the dynamic value of the centripetal force, you need to measure   Mv²/r   .  This is done by measuring r (see Q-1)   and the period T. 
(Q-2) Derive the following expression for the dynamic value of the centripetal force in terms of the measured quantities M, r and T:

F = 4π²  Mr/T²   . (3)

(Q- 3) Measure M:   Again, we can state the precision of our readings by assuming  only an “instrument” uncertainty  due to   random errors from just reading the instrument.  We will assume that the accuracy of any single reading with a mass scale  is plus or minus ¼ of the smallest scale division of  0.1 g. See page 36 here: http://dept.physics.upenn.edu/~uglabs/lab_manual/Lab_Manual.pdf

Thus , ΔM_inst =  0.1/4 = 0. 025 = 0.03 for a single reading with  a mass scale.  But the measurement  may be “non-simple . We thus make the M measurement  taking 5 readings. In this case, we  state the precision by taking  the difference between the minimum and maximum values  and dividing by N (where N = 5.)  We call this quantity R/N.   Compute R/N .  Compute the average (M_BEST) of the 5 measured masses. The uncertainty  you choose will be  either  ΔM _inst or R/N , which ever is larger.  In either case, the uncertainty is rounded to just one digit and we round the average (“best”) value to the same decimal place. The result is reported as M_BEST ± uncertainty .

 (Q-4)  Measure  T : Again, we can state the precision of our readings by assuming  only an “instrument” uncertainty  due to   random errors from just reading the instrument.  We will assume that the accuracy of any single reading with a digital timer  scale  is plus or minus 0.001 s or 0.0001 s, depending on its setting. Because you are defining  T from trials involving 25 rotations, then the "instrument" uncertainty is reduced by a factor of 1/n = 1/25, where n = 25 is the number of trials 

ΔT_inst =  0.001 s/ n  or 0.0001 s / n   (4),

depending on its setting.  

In this experimental ,  the timer  setting was for 0.0001 s.   But the measurement  may be “non-simple.” We thus make the T measurement  in  10 readings. In this case, we  state the precision by taking  the difference between the minimum and maximum values  and dividing by N (where N =10.)  We call this quantity R/N.  Compute R/N .   Compute the average (T_BEST) of the 10 measured times.  Each trial is based on rotating the system 25 times. The uncertainty  you choose will be either    ΔT _inst or R/N , which ever is larger.  In either case, the uncertainty is rounded to just one digit and we round the average (“best”) value to the same decimal place. The result is reported as T_BEST ± uncertainty .

(Q-5) Using (Q–1), (Q-3 ) and (Q-4), compute the dynamic value of  F_BEST using equation  (3). For the value of r , M and T use the “best” value computed in  (Q–1), (Q-3 ) and (Q-4)

(Q-6) .    Beginning  with  equations (3), it is easy to derive  with   Math 1 and 3 calculus
the expression for the uncertainty in the dynamic value of the centripetal force you computed in the previous part:





The expression contains the “best “ values from (Q–1), (Q-3 ), (Q-4) and (Q-5).   Δr,  ΔM and ΔT are the uncertainties in (Q–1), (Q-3 ) and (Q-4).

(Q-7)    Apply the following test to determine whether the data from this experiment supports the
the hypothesis idea that the  static and dynamic  measurement yield identical results  :
|F_BEST – m_BEST··g|  < 2(ΔF + Δmg), where Δm is the uncertainty in the hanging mass (Q-1) bringing  the pointer into alignment with  bob. This test will be discussed in further detail.