|
1. †(40) (Note
this problem is similar to #66, †Chapter
2. †Thatís how we roll---my tests are
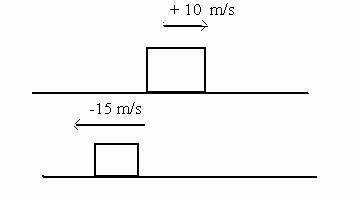
based on the homework.) A car and a truck are moving in opposite† directions on an
isolated† two lane highway.† At t = 0, the truck and car are at the same location (x = 0) along the
x-axis. Assume the positive
x-direction is rightward. †See schematic below.
At t = 0, the truckís velocity is +10.0 m/s. The truck is speeding up with †acceleration †+3.0 m/s2.
At t = 0, the carís velocity -15.0 m/s. The car is
slowing down with† †acceleration +5.0 m/s2.
Show all work clearly.†
(a) (20) What is the DISTANCE between the car and truck †when the car
momentarily comes to rest ?
(b) (15) What is the velocity of the truck when the car comes to rest?
(c) (5) What is the speed of each relative †to the†
other at t = 2.0 seconds?
2. (40 points) ††(Note
this problem is similar to #53, 75, and 38, CH. 2; see also this link
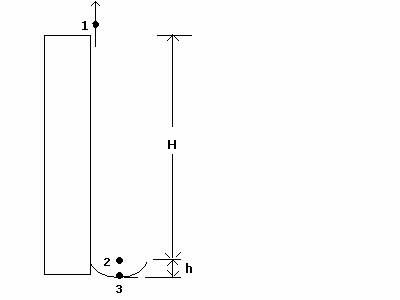
to a problem in purple from Physics 4A--problem 1 at top of page.) †A person jumps vertically† upward with speed |v1| = 4.0 m/s
from the roof† of a building 16.0 m
above a† firefighterís safety net. ††Thus,†
the height H = 16.0 m in the diagram below. The person moves through
the air in free fall,† reaches the net
at point 2† and stretches it †a distance†
h = 1.2 (m) before coming to rest at point 3. Examine the diagram
below for the† various levels† during the †motion. The diagram is not necessarily drawn
to scale.
(a) (15 points) What is the speed of the person when† she reaches the net at point 2?
(b) (15 points) What is the time interval t3
Ė t2 the survivor spends† in
the net ?
(c) (10 points)†
What is the maximum height above the†
net reached by the† personís
feet?
3.††† (40) NOTE:
THIS PROBLEM IS BASED ON LECTURE NOTES, QUIZ 3 AND THE VIRTUAL
LAB WITH SOME
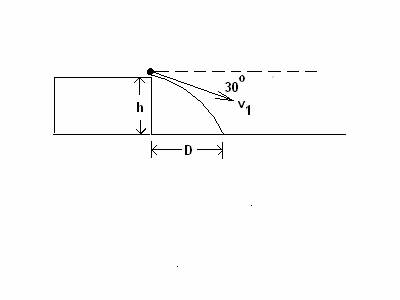
MODIFICATIONS. At t = 0, a ball is launched from the roof of a storage
building that is a distance h† above
the ground. The initial speed of the ball is v1 = 7.00 m/s. The
ball is launched at an initial angle 30 degrees below the horizontal† as
shown.† The ball lands a horizontal
distance D =† 6.0 m from the base of
the building.††
(a) (12) How long (in seconds) does it take the ball
to hit the ground?
(b) (13) What is the height h ( in meters) of the roof ?
(c) (5) What is the x-component of the ballís velocity vector just before
impact?
(d) (5)† What is the y-component of the
ballís velocity vector just before impact?
(e) (5) What is the magnitude of the ballís velocity
vector just before impact? (In other words, use the Pythagorean Theorem to
find the† speed just before impact.)
4.† †(40 points) †Vector Skills.
(a) (16) In the diagram below, 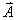 †has magnitude 3.6
m† with the direction shown. †has magnitude 3.6
m† with the direction shown. 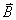 †has magnitude 2.4 m
and points in the 3rd quadrant with direction shown.† Write each vector† component†
in the blanks provided on next page.†
Show work †in spaces below and next pages. †has magnitude 2.4 m
and points in the 3rd quadrant with direction shown.† Write each vector† component†
in the blanks provided on next page.†
Show work †in spaces below and next pages.
(b) (11) Compute the magnitude 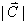 †of the vector sum †of the vector sum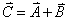 . Show work †in spaces below and next pages . . Show work †in spaces below and next pages .
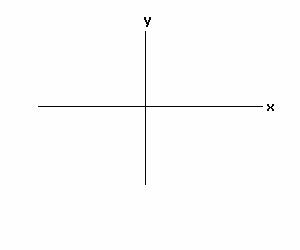
(c) (9) Find the† direction of the
vector sum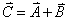 by doing the following: by doing the following:
††††† (i) Show the direction by drawing
this vector sum in the correct quadrant††
on the blank axes provided on next page.
††††† (ii) Calculate the related
(reference) angle 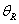 †the vector makes
with the†† x-axis. Show this angle in
sketch, with work. †the vector makes
with the†† x-axis. Show this angle in
sketch, with work. 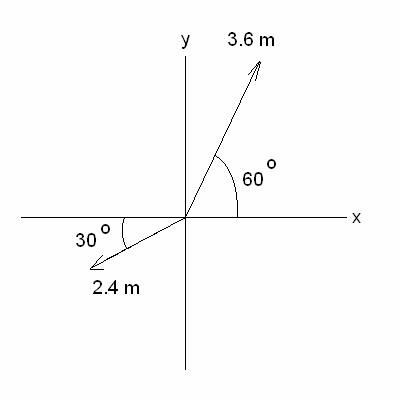
Ax
__________________Ay = ______________________
Bx† _________________By
= _______________________
|




