Lab discussion ; Brightness, Analysis #9. You can reach the same conclusion by looking at the graph, but below is a more quantitative method.
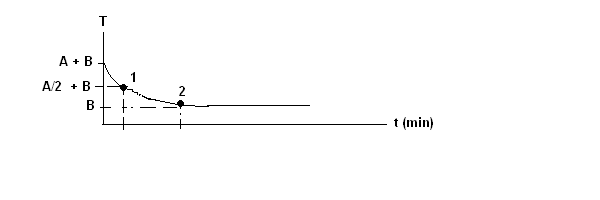
THIS APPROACH ALWAYS WORKS . POINT 1 IS WHEN THE TEMPERATURE IS EXACTLY BETWEEN B AND A + B. Point 2 is when the temperature is 1 degree above B. This is what the question really assumes: The temperature starts out at A/2 units above B. This is what the handout means when it states the thermometer starts out at half the temperature difference between the canister water and the room temperature. Note that A/2 > 1 . Thus A >2 degrees for this universal approach to work.
Find the time period t ' between 0 and 1 and the time period t ' between 1 and 2, and COMPARE.
Get time period t ' between 0 and 1:
A e -at ' + B = A/2 + B
e -at ' = 1/2 or at' = ln (2)
For the time period between 1 and 2, consider t' to be zero when the value of the temperature is (A/2) + B.
In this case, we can write the temperature as T = (A/2) * e -at ' + B . Get time period t ' between 1 and 2:
(A/2) * e -at ' + B = B + 1
(A/2) * e -at ' = 1 .
at' = ln (A./2), where A > 2 . This assures a positive value of t '.
Mathematically, in general these two values of at', ln (2) and ln (A / 2), are NOT equal, so generally it does not take half as long to go from point 1 to 2 as to go from 0 to point 2.