TAKEHOME TEST 3

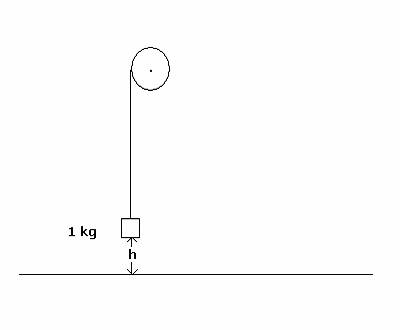
1. CH. 7 (50 POINTS)  A 0.145 - kg ball is thrown upward with speed  v₁ = 16.0 m/s. At a certain vertical height H, the ball has speed v₂ = 2.00 m/s. As it rises to height H,  the force of  air friction does work of magnitude 4.00 J on the ball.  

(a)   (8) What is the direction of the air friction force on the ball, up or down?
(b)   (7) Is the work done by the air friction force positive or negative? Explain briefly.  
(c )  (10) Is the work done by the gravitational force on the ball positive or negative? Explain briefly.  

(d )  (20)  What is the height H?  For full credit you must use either the work energy theorem or conservation of energy in your solution.

(e)   (5) Assume the air friction force is constant. In parts (a) and (b), you addressed the direction of the friction force. In this part, find  the magnitude f_k of the constant  force of air resistance exerted on the ball during its upward motion.

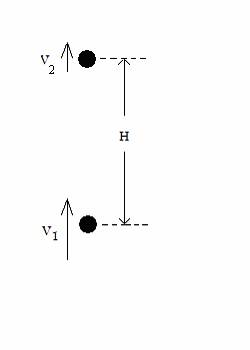
2. CH. 7 (16 POINTS)   A block  of mass M = 1.000 kg has been released from a position above a mass-less,  un-deformed spring with platform. Study the figure below.  Just before the block lands on the spring platform,  its  speed is V₁ . After the  block lands on the platform, it compresses the spring downward a distance h = 0.500 m before momentarily coming to rest. The force constant of the spring is k = 60.00 N/m.
     (a) (4) What is the kinetic energy of the block just before landing on the spring platform? HINT: YOU MAY USE CONSERVATION OF ENERGY;  TAKE INTO ACCOUNT THE GRAVITATIONAL AND SPRING POTENTIAL ENERGIES . YOU MAY DEFINE THE GRAVITATIONAL POTENTIAL ENERGY TO BE ZERO AT THE INSTANT THE BLOCK FULLY COMPRESSES THE SPRING,  I.E.  AT THE BLOCK’S  LOWEST    VERTICAL LOCATION.

     (b) (4) What is speed V₁ of the block just before landing on the spring platform?
     (c) (4)  What is the work done (in Joules) by the spring during the compression?  Is the spring work positive or negative? Circle one. EXPLAIN BRIEFLY.
     (d)  (4 ) What is the work done (in Joules) by the gravitational  force during the compression?  Is the gravitational  work positive or negative? Circle one. EXPLAIN BRIEFLY.

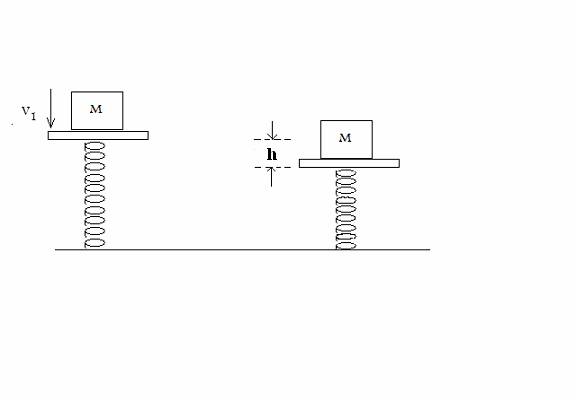
3.  CH. 8 (16 POINTS)  On a frictionless  air track, a 0.5000 kg-glider  moving to the right at 2.950 m/s collides with a 4.0000 kg  glider at rest.   The collision is elastic. Assume the right  direction is the positive direction of motion .

(a) (5 points) What is the velocity  of the  0.5000 kg-glider after the collision? Indicate the direction of motion after the collision, right or left. Is the velocity positive or negative?

(b) (5 points) What is the velocity of the  4.0000 kg-glider after the collision? Indicate the direction of motion after the collision, right or left. Is the velocity positive or negative?

(c) (3 points) Using the velocities of parts (a) and (b), compute the total kinetic energy of the system after the collision.  Do not round off during intermediate computations.

(d) (2 points) Using the initial velocity of 0.500-kg block before the collision,  compute the kinetic energy  before the collision.  Do not round off during intermediate computations.

(e) (1 points) Are the answer to parts (c)  and (d) equal? Should they be equal ? Explain.

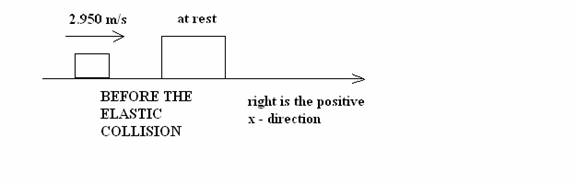
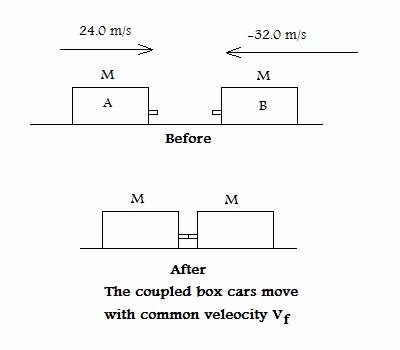
4.  CH. 8 ( 40 points) Two identical box cars of mass M are traveling in opposite directions as shown below. Car A is traveling  right with positive velocity + 24.0 m/s , and car B is traveling left with negative velocity – 32.0 m/s. The velocities are shown below before the perfectly inelastic collision.

During  the collision, the cars lock together and the coupled cars move together with a common velocity.

(a)  (5) What direction do the coupled cars move after the collision right or left?  Circle one.

(b) (20 ) What is the common velocity V_f  after the collision?

FOR THE NEXT PARTS ASSUME M = 1.000 kg. 

(c)  (5 points) Using the velocity of part (b), compute the total kinetic energy of the system after the collision.  Do not round off during intermediate computations.

(d) (5 points) Using the initial velocities of the blocks before the collision,  compute the kinetic energy  before the collision.  Do not round off during intermediate computations.

(e) (5 points) How much energy is lost to heat during the collision?  

5.  CH. 9 (12  points)   An airplane propeller speeds up in its rotation with uniform angular acceleration  α = 1256.00 rad/s². It is  rotating counter clockwise and at t = 0 has an angular speed of  ω_i = 6280.00 rad/s.   

(a)  (4  points)  How many seconds does it take the propeller to reach an angular speed of 16,700.00 rad/s?     
(b)  (4  points)  What is the angular speed (in rad/s) at t = 10.00 seconds?

(c)  (4 points)   Through how many revolutions does the propeller turn in the time interval between 0 and 10.00 seconds?

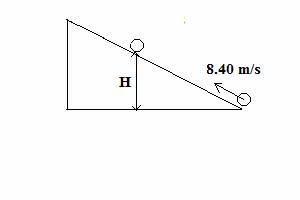
6. CH. 9 (12  points)   A uniform solid sphere of radius R = 0.200 m  and mass M = 1.80 kg starts from the bottom of an   inclined plane  and rolls up the incline without slipping.  The initial translational speed of the center of mass of the sphere  is v_{i cm} = 8.40 m/s.  Show all work.

(a)  (4 points) What is the initial angular velocity ω_i of the sphere at the bottom?
(b)  (4 points) What  is the  total kinetic energy at the bottom? 
(c)  (4 points)  What is the height vertical  H  the sphere reaches when it momentarily comes to rest?
 

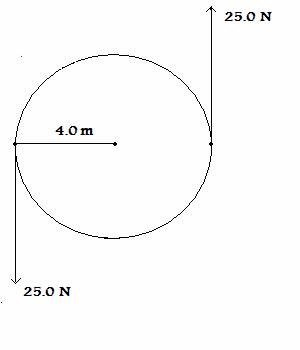
7.  CH. 10 (35 POINTS) A solid, uniform  cylinder  of mass M = 3600 kg and radius R = 4.0 m can rotate about an axis at the center. The cylinder is subjected to the two steady forces applied at the  opposite ends of a diameter shown. As you can see, the forces are tangent to the cylinder rim.
(a) (5) Compute the moment of inertia I about the center.
(b)  (10) What is the magnitude | τ |of the net torque  about the center?
(c)  (10) What is the cylinder’s angular acceleration  α ?
(d)  (10) Assume the  cylinder starts it rotation from rest when subjected to the two steady forces shown.  What is the cylinder’s angular velocity ω after a time period of 60.0 seconds?

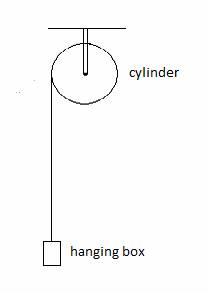
8.  CH. 10 (12 POINTS) A cylinder has R = 0.150 m and mass M_c = 5.00 kg.  The cylinder  turns  without friction about a stationary axle that passes through the center. 

A light rope (of negligible mass) is wrapped around the cylinder and has a 4.00 kg uniform rectangular box  suspended from its free left  end. There is no slippage between rope and the  cylinder surface.     

(a)   (5 points) What is the magnitude τ of the torque on the cylinder about the center?  

(b)   (5 points) What is the magnitude a  of the downward  linear acceleration  of the box?

(c)   (2 points)  Assume the system starts its motion from rest. What is the linear speed of the box after it has descended a distance of
2.0 m? 

9. CH. 9 OR CH. 10 EXTRA CREDIT. (12 POINTS) A 1.000-kg block  hangs vertically at the end of a string wrapped around a pulley of radius R = 0.250 m and mass M = 2.000-kg, The pulley is  shaped in the form of a solid cylinder. Thus, the  pulley has I = ½MR² about the axis of rotation through the center. The vertically hanging block and pulley are shown at the start of the motion when they are released from rest. The block is released from a height h = 1.000 m above the ground.

        What is the linear  speed v of the block just before it hits the ground?